Lösung von Aufgabe 11.3P (SoSe 13)
Aus Geometrie-Wiki
Version vom 12. Juli 2013, 15:08 Uhr von Tutorin Anne (Diskussion | Beiträge)
Beweisen Sie: Bei Spiegelungen, Stöße beim Billard über Bande, etc. gilt stets: Einfallswinkel  gleich Ausfallswinkel
gleich Ausfallswinkel  (siehe GeoGebra-Applet).
(siehe GeoGebra-Applet).
- Vor.: Strecke CED ist die kürzeste Verbindung
- Beh.: Einfallswinkel= Ausfallswinkel
- Beweis:
* 1) S(ab) (C)= C´ Vor., Def. Sg
- 2)
 ist kongruent zu Alpha` WINKELtreue, (1)
ist kongruent zu Alpha` WINKELtreue, (1)
mit Alpha`= <AEC`
- 3) Alpha` ist kongruent
 (2), Scheitelwinkelsatz
(2), Scheitelwinkelsatz
- 4)
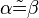 Transitivität d. Winkelkongruenz, (3), (2)
Transitivität d. Winkelkongruenz, (3), (2)
- 5) Einfallswinkel = Ausfallswinkel (4)
--Blumenkind 11:22, 12. Jul. 2013 (CEST)Blumenkind 11:19Uhr, 12.Juli
SPITZE! --Tutorin Anne 16:08, 12. Jul. 2013 (CEST)

