Lösung von Aufgabe 11.5P (SoSe 13)
Zeigen Sie, dass die Verkettung einer Drehung 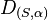 mit einer Verschiebung wieder eine Drehung
mit einer Verschiebung wieder eine Drehung 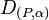 ergibt. Wo liegt das neue Drehzentrum P?
ergibt. Wo liegt das neue Drehzentrum P?
Vor.:
Sa∘Sb∘Sc∘Sd
mit Sa∘Sb ≔ D(S,α) mit a ∩ b = {S} ∧ |∠ab| = α
mit Sc∘Sd ≔ Verschiebung mit c || d --Nolessonlearned 14:08, 12. Jul. 2013 (CEST)
Beh.: D(P,α)
mit Sa'∘Sd' ∧ a' ∩ d' = {P} ∧ |∠ab| ≌ |∠a'd'|--Nolessonlearned 14:08, 12. Jul. 2013 (CEST)
| Beweisschritte | Begründung | |
|---|---|---|
| 1) | Sa∘Sb∘Sc∘Sd | Voraussetzung |
| 2) | Sa'∘Sb'
mit |∠ab| ≌ |∠a'b'| und b' || c |
(1); Vor.; Winkelkongruenz;
Eigenschaft der Drehung |
| 3) | Sc'∘Sd'
mit c' = b' (Identität) mit |cd| = |c'd'| mit c' || d' |
(2); Vor.; Eigenschaft der Verschiebung |
| 4) | Sa'∘Sd' ≔ D(P,α)
mit a' ∩ d' = {P} mit |∠a'd'| = |∠ab| = α |
(1); (2); (3); Vor. |
So kannst du das beweisen. Allerdings lassen sich die Schritte 2 und 3 nicht aus den Definitionen der Drehung und Verschiebung ableiten, sondern aus Sätzen (z.B. Satz IX. 2). Deshalb musst du Eigenschaften der Drehung bzw. Verschiebung schreiben. Bei Schritt 4 fände ich ganz schön, wenn du noch begründest, warum du Spiegelung an Gerade b' und c' weggelassen hast. Dies ist vielleicht sogar in einem zusätzlichen Schritt vor 4.) übersichtlicher.--Tutorin Anne 16:06, 12. Jul. 2013 (CEST)
- Hallo Anne, erstmal danke für deine Hilfe. Schau dir bitte bei Gelegenheit auch die Zusatzaufgaben an. Bin auf deine Mithilfe angewiesen, da sich meine Lerngruppe aufgelöst hat. So nun zur Aufgabe. Ich dachte das die Erwähnung in Schritt 3, dass b' und c' identisch sind als Begründung ausreichend sei.--Nolessonlearned 16:28, 12. Jul. 2013 (CEST)
- Hallo Nolessonlearned, nur weil zwei Geraden identisch sind, heißt das nicht, dass sie sich in Luft auflösen. Entscheidend ist, dass man die Spiegelungen an den jeweiligen Geraden weglassen kann, aber warum???--Tutorin Anne 17:23, 12. Jul. 2013 (CEST)

