Lösung von Zusatzaufgabe 11.2P (SoSe 13)

Beweisen Sie Satz IX.9:
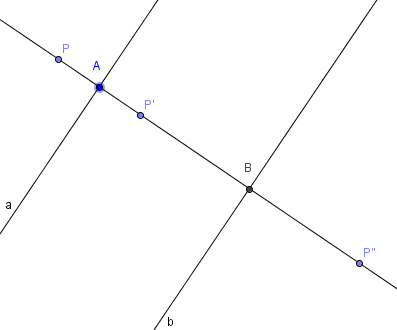
Gegeben seien zwei zueinander parallele Spiegelgeraden a und b. Wir betrachten die Verkettung $S_{a}\circ S_{b}$. Jeder Punkt P hat dabei zu seinem Bildpunkt $P''=S_{a}\circ S_{b}(P)$ einen Abstand der doppelt so groß ist wie der Abstand der beiden Spiegelgeraden.

Hinweis: Hier genügt ein exemplarischer Beweis für eine mögliche Lage von P. Nehmen wir doch mal an, P und seine Spiegelpunkte liegen so:

--Tutorin Anne 17:30, 12. Jul. 2013 (CEST)

Voraussetzung	...
Behauptung	....

Nr.	Beweisschritt	Begründung
1	...)	...
2	...	...
3	...	...
4	...	...
...	...	...
...	...	...