Lösung von Zusatzaufgabe 11.2P (SoSe 13)
Beweisen Sie Satz IX.9:
Gegeben seien zwei zueinander parallele Spiegelgeraden a und b. Wir betrachten die Verkettung 
. Jeder Punkt P hat dabei zu seinem Bildpunkt 
einen Abstand der doppelt so groß ist wie der Abstand der beiden Spiegelgeraden.
Hinweis: Hier genügt ein exemplarischer Beweis für eine mögliche Lage von P. Nehmen wir doch mal an, P und seine Spiegelpunkte liegen so:
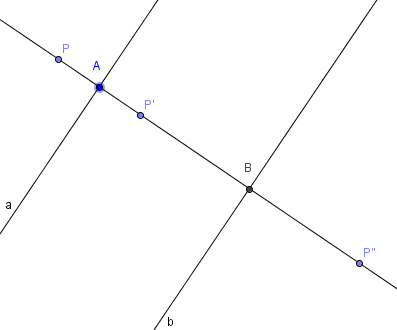
--Tutorin Anne 17:30, 12. Jul. 2013 (CEST)
| Voraussetzung | aIIb, Sa o Sb (P) = P``, g senkrecht zu a, g senkrecht zu b sowie g geschnitten a= (A) und g geschnitten b = B, |
| Behauptung | Abstand ist doppelt groß von P zu P`` |
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | Sa(P)=P´und Sb(P`)=P``mit P, P`und P``Element g | Def. Sg., Vor. |
| 2 | IStrecke PAI= IAP`I und IP`BI=IStreckeBP`Ì sowie PP`senkrecht a und P`P``senkrecht g | (1), Voraussetzung, Konstruktion |
| 3 | P``ist eine Verschiebung in Richtung PP``und PP``ist Richtungsgleich zu AB | (2), Vor. |
| 4 | ... | ... |
| ... | ... | ... |
| ... | ... | ... |
Jetzt weiss ich net wie ich es schreiben soll dass der Abstand doppelt so groß ist. Ich weis das die Verkettung zweier Geradenspiegelungen an parallelen Geraden durch eine Verschiebung ersetzt werden können. Aber wie soll ich es anwenden. ?? Kann mir jemand helfen??;-///--Blumenkind 23:52, 12. Jul. 2013 (CEST)Blumenkind 23:50, 13.Juli
Deinen Beweis hast du gut angefangen. Es ist besser Schritt 2) aus der Def. Geradenspiegelung abzuleiten, in der steht, dass Punkte immer senkrecht zur Symmetrieachse gespiegelt werden und deshalb alle Punkte senkrecht auf a und b stehen und kollinear sind. In der Voraussetzung ist es besser A und B als Schnittpunkte der STrecke PP´´ zu nennen und die Gerade g weg zu lassen, da man sonst eigentlich auch begründen müsste, warum die Punkte P, P´und P´´ auf g liegen. Aber das gäbe keinen Abzug in der Klausur.
Schritt 3 hilft dir nicht weiter. Du musst stadtdessen die Idee wie Nolessonlearnd unten verfolgen.--Tutorin Anne 08:56, 15. Jul. 2013 (CEST)
Sorry, habe währenddessen eine eigene Version erarbeitet.
Ist eine solche ausführliche Voraussetzung erlaubt?
Erwünscht sogar, sofern du alle Schritte zur weiteren Begründung brauchst!--Tutorin Anne 08:56, 15. Jul. 2013 (CEST)
Der Beweis ist sehr lang geworden.
--Nolessonlearned 00:00, 13. Jul. 2013 (CEST)
Voraussetzung:
Sa∘Sb(P) = P´´ mit a || b
mit koll(P,P',P´´)
mit P,P',P ∈ g
mit g ⊥ a ∧ g ⊥ b
mit g ∩ a = {M} ∧ g ∩ b = {N} --Nolessonlearned 18:17, 12. Jul. 2013 (CEST)
Behauptung:
|P͞P´´)| = 2|ab| ≌ 2(|MP'| + |P'N|) --Nolessonlearned 18:17, 12. Jul. 2013 (CEST)
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | koll(P,P',P´´,M,N) | Eigenschaft GS; Voraussetzung |
| 2) | P' = Sa(P) | Def. GS; Voraussetzung |
| 3) | P´´ = Sb(P') | Def. GS; Voraussetzung |
| 4) | P͞M͞| = |M͞P͞'| | (1); (2); Voraussetzung; Streckentreue d. GS bzw. Abstandserhaltung |
| 5) | P͞'N͞| = |N͞P͞`´| | |
| 6) | M͞P͞'| + |P͞'N͞| = |ab| | (1); (4); (5); Streckenaddition bzw. Abstandsaddition; Rechnen in ℝ |
| 7) | P͞M͞| + |N͞P͞``| = |M͞P͞'| + |P͞'N͞| | (4); (5); (6); |
| 8a) | P͞M͞| + |M͞P͞'| + |P͞'N͞| + |N͞P͞``| = |P͞P͞``| | (1); (4); (5); (6); (7); Streckenaddition; Rechnen in R |
| 8) | M͞P͞'| + |P͞'N͞|)2 = |P͞P͞``| | (6); (7); |
| 9) | P͞P͞´´| = 2|ab| | (6); (7); (8) q.e.d |
Die Tabelle stellt leider nicht alle Eingaben korrekt dar. Ich verstehe nicht woran es liegen könnte. In der Vergangenheit hat es immer normal funktioniert.--Nolessonlearned 00:17, 13. Jul. 2013 (CEST)
Hallo Nolessonleard, dein Beweis stimmt. Schritt 8 kann ich nicht aus (6) und (7) nachvollziehen - es ist besser nochmal zu nennen, aus welchen Abständen sich die Strecke zusammensetzt.
GANZ WICHTIG. Abstände sind nicht kongruent, sondern gleich, da es ja reele Zahlen sind. Winkel oder Strecken können kongruent sein, dann dürfen aber keine Betragsstriche und keine Rechenoperationen in dieser Zeile vorkommen.
Die Vorraussetzung kannst du schon so detailliert schreiben. Streng genommen, müsstest du einiges davon eher als Beweisschritte nennen. Das ist aber nicht so wichtig, du kannst auch einfach weniger schreiben und dich auf die Skizze beziehen. Die Gerade g hast du z.B. gar nicht mehr für deinen Beweis gebraucht.--Tutorin Anne 08:48, 15. Jul. 2013 (CEST)
- Vielen Dank für die wertvollen Tipps. --Nolessonlearned 10:42, 15. Jul. 2013 (CEST)
