Lösung von Aufg. 12.06 SoSe 13
Aus Geometrie-Wiki
Version vom 18. Juli 2013, 21:54 Uhr von *m.g.* (Diskussion | Beiträge)
Aufgabe 12.06Beweisen Sie: Die Winkelhalbierenden eines Dreiecks Lösung
Der Rest ergibt sich aus dem Tangentenkrierium und dadurch, dass durch drei nichkollineare Punkte genau ein Kreis bestimmt ist.
--*m.g.* 22:51, 18. Jul. 2013 (CEST) Zurück zu: Serie 12 SoSe 2013 |
 schneiden sich in genau einem Punkt
schneiden sich in genau einem Punkt  , welcher der Mittelpunkt des Inkreises von
, welcher der Mittelpunkt des Inkreises von 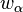 und
und 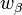 in genau einem Punkt
in genau einem Punkt  schneiden. Sollte dem nicht so sein wären die durch
schneiden. Sollte dem nicht so sein wären die durch 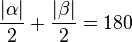 , was ein Widerspruch zur Innenwinkelsumme im Dreieck wäre.
, was ein Widerspruch zur Innenwinkelsumme im Dreieck wäre.
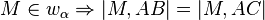 (Winkelhalbierendenkriterium)
(Winkelhalbierendenkriterium)
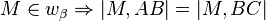 (Winkelhalbierendenkriterium)
(Winkelhalbierendenkriterium)
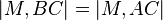 (1 und 2)
(1 und 2)
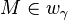 (3 und Winkelhalbierendenkriterium)
(3 und Winkelhalbierendenkriterium)

