Lösung von Aufgabe 10.2
Aus Geometrie-Wiki
Version vom 1. Juli 2010, 18:14 Uhr von Löwenzahn (Diskussion | Beiträge)
VSS: 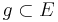 ,
, 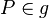
Beh: es gibt genau eine Gerade s durch P, die senkrecht auf g steht
EXISTENZ
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | in  gibt es einen Strahl mit gibt es einen Strahl mit 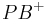
|
Axiom I.2 und Def. Halbgerade |
| (II) | es existiert genau ein Strahl 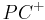 in der Halbebene in der Halbebene 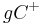 mit mit 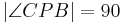
|
Winkelkonstruktionsaxiom, (I) |
| (III) | es exisitiert genau eine Gerade s durch  und und  , senkrecht auf , senkrecht auf 
|
Axiom I.1, (II) |
EINDEUTIGKEIT
Da es nach dem Winkelkonstruktionsaxiom genau eine Gerade gibt, die die Eindeutigkeit bereits gezeigt.
qed --Löwenzahn 17:14, 1. Jul. 2010 (UTC)

