Lösung von Aufgabe 10.2
Inhaltsverzeichnis |
Lösung--Schnirch 13:00, 21. Jul. 2010 (UTC)
Voraussetzung: 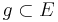 ,
, 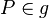
Behauptung: es gibt genau eine Gerade 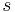 durch
durch  , die senkrecht auf
, die senkrecht auf  steht
steht
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 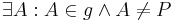
|
Axiom I.2 |
| (II) | 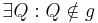
|
Axiom I.3 |
| (III) | In  gibt es genau einen Strahl gibt es genau einen Strahl  mit Anfangspunkt mit Anfangspunkt  derart, dass derart, dass 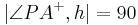
|
Winkelkonstruktionsaxiom, (I), (II) |
| (IV) | Die Gerade 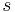 für die gilt: für die gilt: 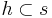 ist die Senkrechte ist die Senkrechte 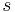 durch durch 
|
(III), (IV), Def. Senkrechte |
| (V) | Die Senkrechte 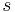 ist eindeutig ist eindeutig
|
Eindeutigkeit des Strahls 
|
vorangegangene Diskussion
Beweis Versuch 1 (verbessert):
VSS: 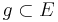 ,
, 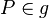
Beh: es gibt genau eine Gerade  durch
durch  , die senkrecht auf
, die senkrecht auf  steht
steht
EXISTENZ
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | Es existiert ein Punkt 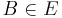 , ,  ungleich ungleich 
|
Axiom I.2 |
| (II) | es existiert ein Punkt 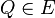 , Q nicht Element g , Q nicht Element g
|
|
| (II) | es existiert ein Punkt 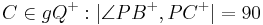
|
Winkelkonstruktionsaxiom, (I), (II) |
| (III) | es exisitiert genau eine Gerade  durch durch  und und  , senkrecht auf , senkrecht auf 
|
Axiom I.1, (II) |
EINDEUTIGKEIT
Da es nach dem Winkelkonstruktionsaxiom genau eine Gerade gibt, ist die Eindeutigkeit bereits gezeigt.
qed --Löwenzahn 17:14, 1. Jul. 2010 (UTC)
Zweiter Beweisversuch (verbessert)
Voraussetzung: g Element E, P Element g Behauptung: s Element g und s senkrecht auf g
Existenz:
| Beweisschritt | Begründung | |
|---|---|---|
| (I) | Es existiert ein X Element E mit der Eigenschaft, dass X Element S und X Element PX+ | Axiom I.2 (Gerade hat mindestens 2 Punkte) |
| (II) | Es existieren auf der Geraden g ein Punkt P1 auf PP1+ und ein Punkt P2 auf PP1- |Winkel(XPP2)| = |Winkel(XPP1)| = |w| mit w = 90 |
Definition V.6 (Rechter Winkel), Axiom IV.3 (Winkeladditionsaxiom) |
| (III) | s steht senkrecht auf g | (II), Definition V.8 (Relation senkrecht) |
Eindeutigkeit: Nach Winkelkonstruktionsaxiom IV.2 gibt es in jeder Halbebene genau nur einen Strahl mit|w|=|Winkel(XPP2)| bzw. |w| = |Winkel(XPP1)| Nach Winkelmaßaxiom IV.1 gibt es für w genau eine reelle Zahl zwischen 0 und 180. Nach der Definition V.6, Satz V.3 und Satz V.4 gibt es rechte Winkel mit der Größe 90. Nach Definition V.8 ist eine Gerade dann senkrecht auf der anderen, wenn bei dem Schnitt der beiden rechte Winkel enstehen. Somit kann es nur einen Strahl geben in jeder Halbebene, der Senkrecht auf g steht und durch den Punkt P geht, da beim Schnitt ein rechter Winkel enstehen muss, der mit der Größe 90 nur einmalig existiert.
Kommentar --*m.g.* 13:51, 2. Jul. 2010 (UTC):
- Die Gerade
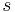 wird mittels des Winkelkonstruktionsaxioms im Laufe des Beweises "generiert". Dementsprechend sollte die Gerade
wird mittels des Winkelkonstruktionsaxioms im Laufe des Beweises "generiert". Dementsprechend sollte die Gerade 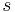 nicht in den Voraussetzungen auftauchen.
nicht in den Voraussetzungen auftauchen.
- Nur mittels einer Definition wird man eine Existenzaussage nicht begründen können. Definitionen mögen zwar alles mögliche festlegen können, ob die Dinge dann auch existieren steht auf einem anderen Blatt. Wir hätten sonst auch beweisen können: Behauptung: Es existieren rechte Winkel. Begründung: Weil rechte Winkel definiert wurden müssen sie auch existieren.

