Übung 2
Aus Geometrie-Wiki
Version vom 16. November 2013, 19:34 Uhr von *m.g.* (Diskussion | Beiträge)
Falkonstruktion der Ellipse
Aufgabe 1
Es sei 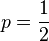 ,
, 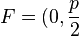 . Die Gerade
. Die Gerade  sei durch die Gleichung
sei durch die Gleichung 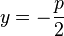 gegeben.
gegeben. 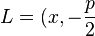 sei ein beliebiger Punkt auf
sei ein beliebiger Punkt auf  . Der Punkt
. Der Punkt  sei der Schnittpunkt der Mittelsenkrechten
sei der Schnittpunkt der Mittelsenkrechten  von
von 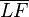 mit der in
mit der in  auf
auf  errichteten Senkrechten
errichteten Senkrechten  .
.
Man beweise:  ist Tangente an die Normalparabel
ist Tangente an die Normalparabel 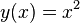 in
in  .
.

