14)
Aus Geometrie-Wiki
Version vom 10. Februar 2014, 08:17 Uhr von EarlHickey (Diskussion | Beiträge)
Beweisen Sie Satz IX.9:
Gegeben seien zwei zueinander parallele Spiegelgeraden a und b. Wir betrachten die Verkettung  . Jeder Punkt P hat dabei zu seinem Bildpunkt
. Jeder Punkt P hat dabei zu seinem Bildpunkt  einen Abstand der doppelt so groß ist wie der Abstand der beiden Spiegelgeraden.
einen Abstand der doppelt so groß ist wie der Abstand der beiden Spiegelgeraden.
- (1)
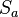 bildet
bildet  auf
auf 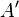 ab und
ab und
- (2)
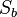 bildet
bildet 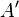 auf
auf 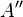 ab.
ab.
- (3) Der Abstand von
 zur Spiegelgeraden
zur Spiegelgeraden  ist gleich dem Abstand von
ist gleich dem Abstand von 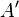 zu
zu  . | (1); Eig. der Geradenspiegelung;
. | (1); Eig. der Geradenspiegelung;
- (4) Der Abstand von
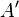 zu
zu  ist gleich dem Abstand von
ist gleich dem Abstand von 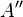 zu
zu  . | (2); Eig. der Geradenspiegelung;
. | (2); Eig. der Geradenspiegelung;
- (5) Der Abstand von
 zu
zu  ist somit gleich dem Abstand von
ist somit gleich dem Abstand von 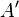 zu
zu 
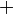 dem Abstand von
dem Abstand von 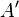 zu
zu  . | (3); (4);
. | (3); (4);
- (6) Das ist Gleich der Summe der Abstände von
 zur Spiegelgeraden
zur Spiegelgeraden 
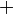 dem Abstand von
dem Abstand von 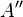 zu
zu  |(3); (4); (5);
|(3); (4); (5);
- --EarlHickey (Diskussion) 08:17, 10. Feb. 2014 (CET)
- (1)

