Aufgabe 2
Aus Geometrie-Wiki
Version vom 9. November 2016, 20:24 Uhr von AlanTu (Diskussion | Beiträge)
Satz: In einem Dreieck  mit
mit 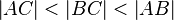 sind die Winkel
sind die Winkel  und
und  nicht kongruent zueinander.
nicht kongruent zueinander.
Inhaltsverzeichnis |
a) Welcher Beweis ist korrekt?
Begründen Sie ausführlich! (Der Basiswinkelsatz und seine Umkehrung seien bereits bewiesen.)
Beweis 1
Sei  ein Dreieck.
ein Dreieck.
- Voraussetzung
-
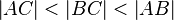 .
.
- Behauptung
-
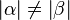
- Beweis
-
Da nach Voraussetzung
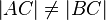 gilt, folgt nach dem Basiswinkelsatz
gilt, folgt nach dem Basiswinkelsatz 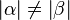 .
.Damit ist der Satz bewiesen.
Beweis 2
Sei  ein Dreieck.
ein Dreieck.
- Voraussetzung
-
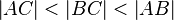 .
.
- Behauptung
-
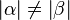
- Beweis
-
Nach Umkehrung des Basiswinkelsatzes gilt: Wenn
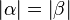 dann gilt
dann gilt 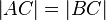 .
.Die Kontraposition der Umkehrung lautet also: Wenn
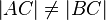 dann gilt
dann gilt 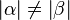 .
.Da die Kontraposition gleichwertig ist, kann man auch diese beweisen.
Da nach Voraussetzung gilt:
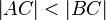 , d.h.
, d.h. 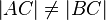 , kann nach Kontraposition der Umkehrung des Basiswinkelsatzes direkt gefolgert werden:
, kann nach Kontraposition der Umkehrung des Basiswinkelsatzes direkt gefolgert werden: 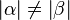 .
.Damit ist der Satz bewiesen.

