Diskussion:Auftrag der Woche 4 (WS 16 17)
Aus Geometrie-Wiki
Version vom 17. November 2016, 13:56 Uhr von AlanTu (Diskussion | Beiträge)
Hallo AlanTu,
ich finde es toll, dass du eine GeoGebra Datei hochgeladen hast.
Sie zeigt durch den Schieberegler und der Spur anschaulich, dass die Mittelsenkrechte eine Punktmenge mit der
oben genannten Eigenschaft ist. Leider bewegen sich aber 2 Punkte in deiner Datei auf der Mittelsenkrechten.
Du hast sie konstruiert als Schnittpunkte der Kreise um A und B.
Anbei habe ich eine GeoGebra Datei erstellt. Überlege, wie habe ich das Problem gelöst?
Gruß Alex--Tutor: Alex (Diskussion) 23:46, 16. Nov. 2016 (CET)
- Hallo Alex,
- danke für dein Feedback zu meiner Lösung. Ich verstehe den Kritikpunkt mit den zwei Punkten, würde das aber weniger als Problem sehen [1]. Je nach Sichtweise mag die Lösung nicht sehr elegant erscheinen, ich halte die Lösung aber immernoch für eine der Eleganteren. Wahrscheinlich kommt das auch auf die Sichtweise auf die Aufgabenstellung an.
- Mein Ansatz war eher, dass ich die gegebene Menge visualisiere, ohne weitere Kenntnisse, also z.B. ohne schon zu wissen, dass die Mittelsenkrechte herauskommt. Dabei habe ich auch ganz vergessen, zu verdeutlichen, dass die Menge genau die Mittelsenkrechte beschreibt. Dazu braucht man dann noch eine weitere Begründung, warum das so ist. Hab mal noch ein paar Absätze ergänzt, wie ich die Konstruktion genau gemeint habe und wie man damit begründen kann, dass die Mittelsenkrechte herauskommt.
- Wenn man die Mittelsenkrechte so als Vereinigung von vielen Teilmengen sieht ist es auch kein Problem mehr, dass es zwei Schnittpunkte gibt. Man „wirft“ einfach beide in die Lösungsmenge während man alle möglichen Kreisradien „ausprobiert“.
- Du hast ja vorausgesetzt, dass die Mittelsenkrechte herauskommt und gezeigt, dass alle Punkte der Mittelsenkrechten in
 liegen, bist also aus der anderen Richtung an das Problem herangegangen. Finde ich auch eine gute Lösung, nur sind daran meiner Meinung nach wiederum zwei andere Dinge unschön:
liegen, bist also aus der anderen Richtung an das Problem herangegangen. Finde ich auch eine gute Lösung, nur sind daran meiner Meinung nach wiederum zwei andere Dinge unschön:
- Dein
 ist ja als Schnittpunkt vom Kreis um den Mittelpunkt von
ist ja als Schnittpunkt vom Kreis um den Mittelpunkt von  und
und  und der Mittelsenkrechten definiert. Da es davon aber zwei gibt, entscheidest du dich immer für einen von beiden. Diese Unterscheidung der beiden Punkte ist ja nicht so ganz ohne weiteres möglich (in Geogebra schon, aber mathematisch muss man ja quasi ein „links“ von
und der Mittelsenkrechten definiert. Da es davon aber zwei gibt, entscheidest du dich immer für einen von beiden. Diese Unterscheidung der beiden Punkte ist ja nicht so ganz ohne weiteres möglich (in Geogebra schon, aber mathematisch muss man ja quasi ein „links“ von  und ein „rechts“ davon definieren, z.B. über den Winkel
und ein „rechts“ davon definieren, z.B. über den Winkel 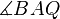 ).
).
- Dass
 negativ werden kann und dann der Betrag für den Radius verwendet wird und das Signum bestimmt, welcher Schnittpunkt ausgewählt wird.
negativ werden kann und dann der Betrag für den Radius verwendet wird und das Signum bestimmt, welcher Schnittpunkt ausgewählt wird.  codiert also den Radius und die „Richtung“ in einer Variablen
codiert also den Radius und die „Richtung“ in einer Variablen
- Dein
- Ich habe mal noch eine weitere Lösung hinzugefügt, die den Kritikpunkten beider Seiten begegnen soll. Es gibt immer genau einen Wert für jeden Wert des Schiebereglers, es ist kein Entscheiden zwischen mehreren Schnittpunkten nötig und der Schieberegler codiert nicht mehrere Variablen, sondern einfach den Winkel zweier Geraden gegenüber der Strecke
 .
.
- ↑ oder beziehst du dich oben mit dem Wort Problem auf die Aufgabenstellung als mathematisches Problem?

