Didaktik der Bruchrechnung
Aus Geometrie-Wiki
Version vom 21. Februar 2017, 12:58 Uhr von *m.g.* (Diskussion | Beiträge)
Inhaltsverzeichnis |
Fachliche Grundlagen
Bruchbegriff
Äquivalenzrelationen
Reflexivität
Jedes Element steht zu sich selbst in Relation.
Symmetrie
Wenn a in Relation zu b, dann auch b in Relation zu a.
Transitivität
Wenn a in Relation zu b und b in Relation zu c, dann a in Relation zu c.
Beispiele:
Parallelität von Geraden, Gleicheitsrelation (=), Quotientengleichheit für Brüche,
Gegenbeispiele
senkrecht auf der Menge der Geraden (Reflexivität und Transitivität verletzt)
Klasseneinteilungen
Brüche
Jeder Bruch ist ein geordnetes Paar von natürlichen Zahlen z und n, das in der Form 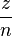 gechrieben wird.
gechrieben wird.
gebrochene Zahlen bzw. Bruchzahlen
Unter einer gebrochenen Zahl versteht man eine Menge von Brüchen, die durch Kürzen oder Erweitern auseinander hervorgehen.
Relation: (quotientengleich)
Zwei Brüche 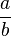 und
und 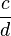 heißen quotientengleich, wenn
heißen quotientengleich, wenn
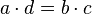 gilt.
gilt.

