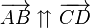Strecken, Pfeile und Pfeilklassen SoSe 2017
Aus Geometrie-Wiki
Version vom 4. Juni 2017, 11:54 Uhr von *m.g.* (Diskussion | Beiträge)
StreckenDefinitionDefinition: (Strecke
BemerkungIm Gegensatz zur Definition des Begriffs Strecke in der Einführung in die Geometrie lassen wir hier zu, dass die Punkte gerichtete Strecken bzw PfeileDefinition: (gerichtete Strecke
PfeilklassenDefinition: (Pfeilgleichheit)
|
 )
)
 und
und  zwei beliebige Punkte. Unter der Strecke
zwei beliebige Punkte. Unter der Strecke 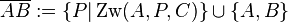 .
.
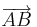 )
)
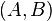 und nennen
und nennen 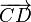 stehen in der Relation pfeilgleich zueinander, wenn
stehen in der Relation pfeilgleich zueinander, wenn 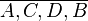 ein Parallelogramm ist. In Zeichen:
ein Parallelogramm ist. In Zeichen: