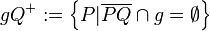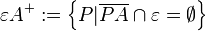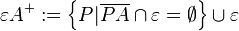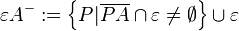Lösung von Aufgabe 7.03 SoSe 2017
Aus Geometrie-Wiki
Version vom 22. Juni 2017, 15:53 Uhr von 1.11.21.1211.111221.312211.13112221 (Diskussion | Beiträge)
|
Es sei Lösung 1Definition offener Halbebene: Zweckdienliche Umformung für den Raum: Zum Schluss und damit auch dem Abschluss der Halbräume noch
Lösung 2 |
 eine Ebene und
eine Ebene und  ein Punkt außerhalb von
ein Punkt außerhalb von 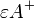 und Halbraum
und Halbraum 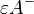 .
.