Lösung von Aufgabe 12.6
Aus Geometrie-Wiki
Version vom 14. Juli 2010, 12:07 Uhr von Löwenzahn (Diskussion | Beiträge)
Beweisen Sie: Wenn  ein Punkt außerhalb der Geraden
ein Punkt außerhalb der Geraden  ist, dann gibt es eine Gerade
ist, dann gibt es eine Gerade  , die durch
, die durch  geht und parellel zu
geht und parellel zu  ist.
ist.
Versuch 1
VSS: Punkt  , Gerade
, Gerade  ,
, 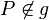
Beh: Gerade  ,
, 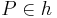 ,
, 
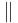

| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 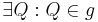 , , 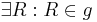
|
(Axiom I.0) |
| (II) | Gerade PQ | (Axiom I.1) |
| (III) | das Maß von 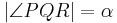 im Punkt im Punkt  an Gerade an Gerade 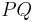 in der Halbebene in der Halbebene 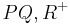 abtragen. Es exisitert genau ein abtragen. Es exisitert genau ein 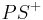 mit dem Maß mit dem Maß 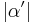 = = 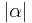
|
(Winkelkonstruktionsaxiom), (Winkelmaßaxiom), (I), (II) |
| (IV) | 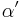 , ,  sind Stufenwinkel sind Stufenwinkel
|
(III), (Def. Stufenwinkel) |
| (V) | 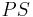 = = 
|
(Axiom I.1) |
| (V) |  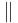 
|
(Umkehrung Stufenwinkelsatz), (IV), (V) |
--> Beh ist wahr.
--Löwenzahn 11:07, 14. Jul. 2010 (UTC)

