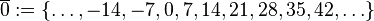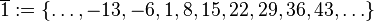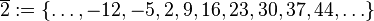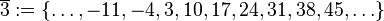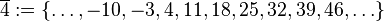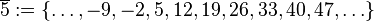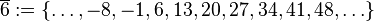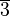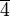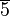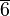Die Gruppe der Restklassen modulo 7 bzgl. der Restklassenmultiplikation

Restklassen modulo 7 In einer Klasse liegen alle ganzen Zahlen, die bei Division durch 7 denselben Rest lassen. Mögliche Reste sind damit 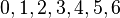$0, 1, 2, 3 ,4, 5, 6$. wir erhalten die folgenden Restklassen: $\overline{0}:=\{\ldots, -14, -7, 0, 7, 14, 21, 28, 35, 42, \ldots \}$ $\overline{1}:=\{\ldots, -13, -6, 1, 8, 15, 22, 29, 36, 43, \ldots \}$ $\overline{2}:=\{\ldots, -12, -5, 2, 9, 16, 23, 30, 37, 44, \ldots \}$ $\overline{3}:=\{\ldots, -11, -4, 3, 10, 17, 24, 31, 38, 45, \ldots \}$ $\overline{4}:=\{\ldots, -10, -3, 4, 11, 18, 25, 32, 39, 46, \ldots \}$ $\overline{5}:=\{\ldots, -9, -2, 5, 12, 19, 26, 33, 40, 47, \ldots \}$ $\overline{6}:=\{\ldots, -8, -1, 6, 13, 20, 27, 34, 41, 48, \ldots \}$ $\odot$ $\overline{1}$ $\overline{2}$ $\overline{3}$ $\overline{4}$ $\overline{5}$ $\overline{6}$ $\overline{1}$ $\overline{1}$ $\overline{2}$ $\overline{3}$ $\overline{4}$ $\overline{5}$ $\overline{6}$ $\overline{2}$ $\overline{2}$ $\overline{4}$ $\overline{6}$ $\overline{1}$ $\overline{3}$ $\overline{5}$ $\overline{3}$ $\overline{3}$ $\overline{6}$ $\overline{2}$ $\overline{5}$ $\overline{1}$ $\overline{4}$ $\overline{4}$ $\overline{4}$ $\overline{1}$ $\overline{5}$ $\overline{2}$ $\overline{6}$ $\overline{3}$ $\overline{5}$ $\overline{5}$ $\overline{3}$ $\overline{1}$ $\overline{6}$ $\overline{4}$ $\overline{2}$ $\overline{6}$ $\overline{6}$ $\overline{5}$ $\overline{4}$ $\overline{3}$ $\overline{2}$ $\overline{1}$