Lösung von Aufgabe 12.10
Aus Geometrie-Wiki
Version vom 14. Juli 2010, 12:20 Uhr von Löwenzahn (Diskussion | Beiträge)
Beweis des Stufenwinkelsatzes:
Es seien a und b zwei zueinander parallele Geraden, die durch eine dritte Gerade c geschnitten werden. Die bei diesem Schnitt entstehenden Stufenwinkel sind kongruent.
Lösung 1
VSS: Gerade 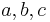 ,
, 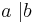 ,
,  schneidet
schneidet  und
und 
Beh: 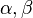 sind Stufenwinkel, oBdA:
sind Stufenwinkel, oBdA: 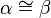
ANN:  >
> 
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 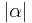 im Scheitelpunkt von im Scheitelpunkt von  in der gleichen Halbebene bzgl in der gleichen Halbebene bzgl  abtragen, es entsteht der Winkel abtragen, es entsteht der Winkel 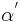
|
(Winkelmaßaxiom), (Winkelkonstruktionsaxiom) |
| (II) | es existiert ein Punkt 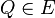 , Q nicht Element g , Q nicht Element g
|
|
| (III) | es existiert ein Punkt 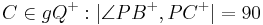
|
Winkelkonstruktionsaxiom, (I), (II) |
| (IV) | es exisitiert genau eine Gerade  durch durch  und und  , senkrecht auf , senkrecht auf 
|
Axiom I.1, (II) |

