Gruppendefinition (Gleichung)
Aus Geometrie-Wiki
Version vom 25. November 2017, 13:01 Uhr von *m.g.* (Diskussion | Beiträge)
Eindeutigkeit des EinslementesSatz 3Jede Gruppe hat genau ein Einslement. Beweis von Satz 3Es sei Eindeutigkeit der inversen ElementeSatz 4In jeder Gruppe Beweis von Satz 4Es sei |
![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe. Nach der Definition des Begriffs Gruppe hat
eine Gruppe. Nach der Definition des Begriffs Gruppe hat 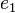 . Es bleibt zu zeigen, dass
. Es bleibt zu zeigen, dass 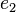 hat. Wir nehmen an es gibt
hat. Wir nehmen an es gibt 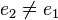 . Nach Satz 2 sind
. Nach Satz 2 sind 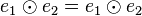 . Aus dieser Gleichung folgt wegen der Einslement eigenschaft beider Elemente
. Aus dieser Gleichung folgt wegen der Einslement eigenschaft beider Elemente 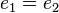 .
.
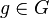 hat genau ein inverses Element.
hat genau ein inverses Element.
 in
in  ein Inverses
ein Inverses 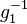 .
.

