Eindeutigkeit des Einslementes
Satz 3
Jede Gruppe hat genau ein Einslement.
Beweis von Satz 3
Es sei ![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe. Nach der Definition des Begriffs Gruppe hat eine Gruppe. Nach der Definition des Begriffs Gruppe hat ![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Einslement eine Einslement 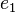 . Es bleibt zu zeigen, dass . Es bleibt zu zeigen, dass ![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) kein weiteres Einslement kein weiteres Einslement 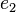 hat. Wir nehmen an es gibt hat. Wir nehmen an es gibt 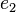 mit mit 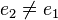 . Nach Satz 2 sind . Nach Satz 2 sind 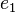 und und 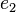 von links und von rechts Einselemente. Wir gehen aus von der Gleichung von links und von rechts Einselemente. Wir gehen aus von der Gleichung 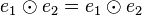 . Aus dieser Gleichung folgt wegen der Einslement eigenschaft beider Elemente . Aus dieser Gleichung folgt wegen der Einslement eigenschaft beider Elemente  und und 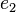 (und das sowohl von rechts, wie auch von links) (und das sowohl von rechts, wie auch von links) 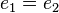 . .
Eindeutigkeit der inversen Elemente
Satz 4
In jeder Gruppe ![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) gilt: Jedes Gruppenelement gilt: Jedes Gruppenelement 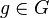 hat genau ein inverses Element. hat genau ein inverses Element.
Beweis von Satz 4
Es sei 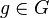 eine Gruppe mit dem Einslement eine Gruppe mit dem Einslement  . Nach der Definition des Begriffs Gruppe hat . Nach der Definition des Begriffs Gruppe hat  in in  ein Inverses ein Inverses  bezüglich bezüglich 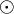 . Wir nehmen an, . Wir nehmen an,  hat in hat in  ein weiteres Inverses ein weiteres Inverses 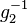 , das natürlich von , das natürlich von  verschieden ist. Nach Satz 1 wissen wir, dass verschieden ist. Nach Satz 1 wissen wir, dass  und und 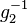 von links und von rechts invers zu von links und von rechts invers zu  bzgl. bzgl. 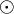 sind. sind.
Die triviale Gleichung 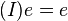 "pumpen" wir zu "pumpen" wir zu 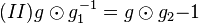 auf. auf.
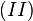 multiplizieren wir auf beiden Seiten von links mit multiplizieren wir auf beiden Seiten von links mit  und erhalten und erhalten 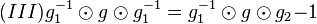 . .
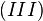 verkürzt sich zu verkürzt sich zu 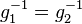 , was ein Widerspruch zu unserer Annahme , was ein Widerspruch zu unserer Annahme 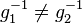 ist. ist.
|