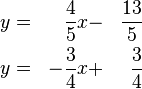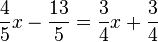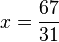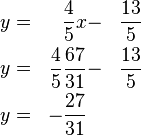Das Wiki für die Lehrveranstaltung "Lineare Algebra/analytische Geometrie", Sommersemester 2017
Literatur
Literatur
Aus früheren Semestern
Kapitel 1: Lineare Gleichungssysteme
Lineare Gleichungssysteme mit zwei Variablen und zwei Gleichungen
Allgemeine lineare Gleichung mit zwei Variablen
ax + by + c = 0
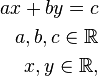
[ www.geogebra.org is not an authorized iframe site ]
Grafische Veranschaulichung der Lösungsmenge einer Gleichung vom Typ ax+by=c
Es seien 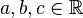 , beliebig aber fest, , beliebig aber fest, 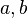 nicht gleichzeitig nicht gleichzeitig 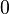 , ,
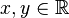 , variabel. , variabel.
Wir untersuchen die Gleichung
(I) 
Satz 1:
- Die Gleichung (II)
 beschreibt die Menge aller Punkte einer Geraden in der reellen Zahlenebene. beschreibt die Menge aller Punkte einer Geraden in der reellen Zahlenebene.
Beweis:
Aus der Schule ist die folgende Gleichung für Geraden bekannt: 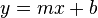 , , 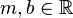 , beliebig aber fest, , beliebig aber fest, 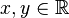 variabel.
Wir führen zwei Beweise: variabel.
Wir führen zwei Beweise:
- Wir zeigen, dass jede Gleichung vom Typ (I) durch äquivalente Umformungen in eine Gleichung vom Typ (II) überführt werden kann.
- Wir zeigen, dass umgekehrt (fast) jede Gleichung vom Typ (II) durch äquivalente Umformungen in den Typ (I) überführt werden können.
Ausführung des Beweises: Übungsaufgaben 1.1 und 1.2 in Serie 1: Geraden in der Ebene, zwei Gleichungen mit zwei Unbekannten SoSe 2018
Algebraische Beschreibung der Lösungsmenge einer Gleichung der Form 
Voraussetzung
Wir schließen aus, dass  und und  gleichzeitig gleichzeitig 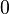 sind: sind: 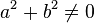
Fall 1: 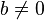
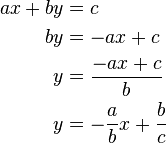
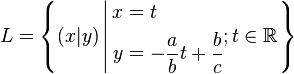
Falls 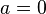 vereinfacht sich die Lösungsmenge vereinfacht sich die Lösungsmenge  zu: zu:
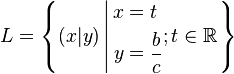
Fall 2: 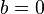
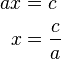
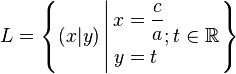
Zusammenfassung
-
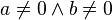 :Gerade, die weder zur :Gerade, die weder zur 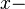 noch zur noch zur 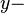 Achse parallel ist. Achse parallel ist.
-
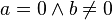 : Gerade, die parallel zur : Gerade, die parallel zur 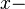 Achse ist. Achse ist.
-
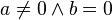 : Gerade, die parallel zur : Gerade, die parallel zur 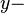 Achse ist. Achse ist.
Lösen eines linearen Gleichungssystems mit zwei Gleichungen und zwei Unbekannten
Das Gleichsetzungsverfahren
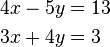
Wir stellen beide Gleichungen nach 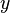 um: um:
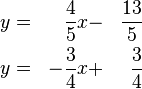
Gleichsetzen der rechten Seiten:
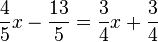
Vereinfachen:
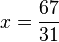
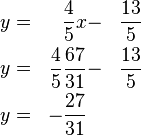
[ www.geogebra.org is not an authorized iframe site ]
Das Additionsverfahren
Äquivalenzumformungen für Lineare Gleichungssysteme
- Vertauschen zweier Gleichungen
- Multiplikation einer Gleichung mit einer reellen Zahl
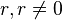
- Addition zweier Gleichungen
Beispiel 1
Fehler beim Parsen(Lexikalischer Fehler): \begin{align} \text{(I)} && 5x + 7y &= 4 && \\ \text{(II)} && 3x + 11y &= 1 && \\ \hline \text{(I)} && 5x + 7y &= 4 && \vert : 5\\ \text{(II)} && 3x + 11y &= 1 && \\ \hline \text{(I')} && 1x + \frac{7}{5}y &= \frac{4}{5} && \\ \text{(II)} && 3x + 11y &= 1 && \\ \hline \text{(I')} 1x + \frac{7}{5}y &= \frac{4}{5} && \\ \text{(II-3 \cdot I')} && - 34y &= 7 && \\ \hline \text{(I)} && 5x + 7y &= 4 && \vert :(-7) \\ \text{(II'')} && y &= -\frac{7}{34} && \\ \hline \text{(I'')} && -\frac{5}{7}x - y &= -\frac{4}{7} && \\ \text{(II'')} && y &= -\frac{7}{34} && \\ \hline \text{(I''+ II'')} && -\frac{5}{7}x ~ ~ ~&= -\frac{4}{7}-\frac{7}{34} && \\ \text{(II'')} && y &= -\frac{7}{34} && \\ \hline \text{(I''')} && x ~ ~ ~&= \frac{37}{68} && \\ \text{(II'')} && y &= -\frac{7}{34} && \\ \hline \end{align}
| 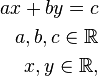
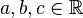 , beliebig aber fest,
, beliebig aber fest, 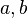 nicht gleichzeitig
nicht gleichzeitig 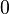 ,
,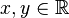 , variabel.
, variabel.
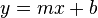 ,
, 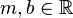 , beliebig aber fest,
, beliebig aber fest,  und
und  gleichzeitig
gleichzeitig 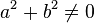
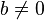
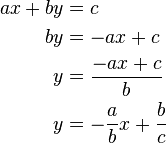
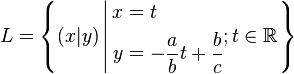
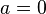 vereinfacht sich die Lösungsmenge
vereinfacht sich die Lösungsmenge  zu:
zu: 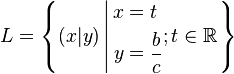
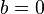
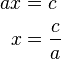
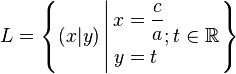
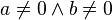 :Gerade, die weder zur
:Gerade, die weder zur 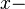 noch zur
noch zur 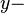 Achse parallel ist.
Achse parallel ist.
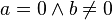 : Gerade, die parallel zur
: Gerade, die parallel zur 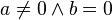 : Gerade, die parallel zur
: Gerade, die parallel zur 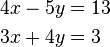
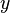 um:
um: