Aufgabe 1.1
Unter der symmetrischen Gruppe 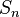 versteht man die Gruppe der Permutationen von versteht man die Gruppe der Permutationen von  Elementen bezüglich der NAF von Permutationen.
Generieren Sie die Verknüpfungstabelle der Elementen bezüglich der NAF von Permutationen.
Generieren Sie die Verknüpfungstabelle der  . .
Aufgabe 1.2
Die symmetrische Gruppe 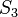 besteht aus 6 Permutationen. Interpretieren Sie die besteht aus 6 Permutationen. Interpretieren Sie die 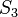 als Deckabbildungsgruppe eines regelmäßigen n-Ecks. als Deckabbildungsgruppe eines regelmäßigen n-Ecks.
Aufgabe 1.3
Unter 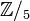 verstehen wir alle Restklassen modulo verstehen wir alle Restklassen modulo 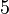 , d.h. in der Klasse , d.h. in der Klasse 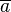 liegen alle ganzen Zahlen die denselben Rest bei Division durch liegen alle ganzen Zahlen die denselben Rest bei Division durch 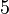 wie die ganze Zahl wie die ganze Zahl  lassen. Die Addition lassen. Die Addition  zweier Restklassen zweier Restklassen 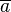 und und 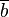 ist wie folgt definiert: ist wie folgt definiert: 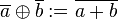 . Beweisen Sie: . Beweisen Sie:
Die Restklassenaddition der Restklassen modulo  ist repräsentantenunabhängig, d.h. es gilt: ist repräsentantenunabhängig, d.h. es gilt:
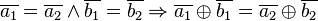
Aufgabe 1.4
Beweisen Sie, dass ![[\mathbb{Z}/_5,\oplus]](/images/math/0/0/4/0043d947e2824153f47941fc1fc6d5d9.png) eine Gruppe ist. eine Gruppe ist.
Aufgabe 1.5
Es sei 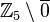 die Menge der Restklassen modulo die Menge der Restklassen modulo 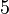 ohne die Klasse ohne die Klasse  . Beweisen Sie, dass diese Menge von Restklassen bzgl. der Retsklassenmultiplikation eine Gruppe bildet. . Beweisen Sie, dass diese Menge von Restklassen bzgl. der Retsklassenmultiplikation eine Gruppe bildet.
Aufgabe 1.6
Es sei ![[\mathbb{N},\cdot]](/images/math/8/f/d/8fd4f4229f12df9ff0dc9d1e91688c5f.png) die Menge der natürlichen Zahlen (ohne Null) zusammen mit der üblichen Multiplikation. Welche Gruppenaxiome sind in die Menge der natürlichen Zahlen (ohne Null) zusammen mit der üblichen Multiplikation. Welche Gruppenaxiome sind in ![[\mathbb{N},\cdot]](/images/math/8/f/d/8fd4f4229f12df9ff0dc9d1e91688c5f.png) erfüllt und welche nicht? erfüllt und welche nicht?
Aufgabe 1.7
Es sei 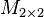 die Menge aller die Menge aller 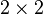 Matrizen ohne die Matrix, die nur aus Nullen besteht. Untersuchen Sie, ob Matrizen ohne die Matrix, die nur aus Nullen besteht. Untersuchen Sie, ob 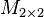 bzgl. der üblichen Matrizenmultiplikation eine Gruppe bildet. bzgl. der üblichen Matrizenmultiplikation eine Gruppe bildet.
Aufgabe 1.8
Geben Sie eine vierelementige Teilmenge aus 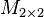 an, die bzgl. der Matrizenmultiplikation eine Gruppe ist. an, die bzgl. der Matrizenmultiplikation eine Gruppe ist.
| 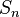 versteht man die Gruppe der Permutationen von
versteht man die Gruppe der Permutationen von  Elementen bezüglich der NAF von Permutationen.
Generieren Sie die Verknüpfungstabelle der
Elementen bezüglich der NAF von Permutationen.
Generieren Sie die Verknüpfungstabelle der  .
.
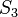 besteht aus 6 Permutationen. Interpretieren Sie die
besteht aus 6 Permutationen. Interpretieren Sie die 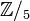 verstehen wir alle Restklassen modulo
verstehen wir alle Restklassen modulo 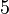 , d.h. in der Klasse
, d.h. in der Klasse 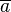 liegen alle ganzen Zahlen die denselben Rest bei Division durch
liegen alle ganzen Zahlen die denselben Rest bei Division durch  lassen. Die Addition
lassen. Die Addition  zweier Restklassen
zweier Restklassen 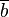 ist wie folgt definiert:
ist wie folgt definiert: 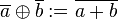 . Beweisen Sie:
. Beweisen Sie: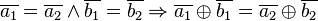
![[\mathbb{Z}/_5,\oplus]](/images/math/0/0/4/0043d947e2824153f47941fc1fc6d5d9.png) eine Gruppe ist.
eine Gruppe ist.
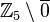 die Menge der Restklassen modulo
die Menge der Restklassen modulo  . Beweisen Sie, dass diese Menge von Restklassen bzgl. der Retsklassenmultiplikation eine Gruppe bildet.
. Beweisen Sie, dass diese Menge von Restklassen bzgl. der Retsklassenmultiplikation eine Gruppe bildet.
![[\mathbb{N},\cdot]](/images/math/8/f/d/8fd4f4229f12df9ff0dc9d1e91688c5f.png) die Menge der natürlichen Zahlen (ohne Null) zusammen mit der üblichen Multiplikation. Welche Gruppenaxiome sind in
die Menge der natürlichen Zahlen (ohne Null) zusammen mit der üblichen Multiplikation. Welche Gruppenaxiome sind in 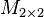 die Menge aller
die Menge aller 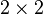 Matrizen ohne die Matrix, die nur aus Nullen besteht. Untersuchen Sie, ob
Matrizen ohne die Matrix, die nur aus Nullen besteht. Untersuchen Sie, ob 
