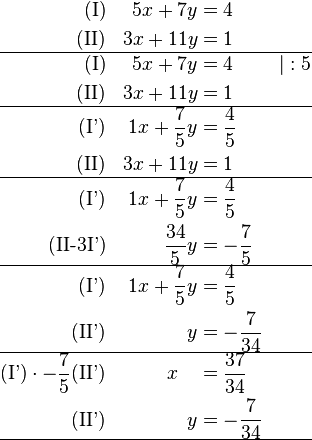analytische Geometrie SoSe 2018
Aus Geometrie-Wiki
Version vom 3. Mai 2018, 15:19 Uhr von *m.g.* (Diskussion | Beiträge)
|
Das Wiki für die Lehrveranstaltung "Lineare Algebra/analytische Geometrie", Sommersemester 2017
LiteraturAus früheren Semestern
Kapitel 1: Lineare GleichungssystemeLineare Gleichungssysteme mit zwei Variablen und zwei GleichungenAllgemeine lineare Gleichung mit zwei Variablen
Lösen eines linearen Gleichungssystems mit zwei Gleichungen und zwei UnbekanntenDas Gleichsetzungsverfahren
Das AdditionsverfahrenÄquivalenzumformungen für Lineare Gleichungssysteme
Beispiel 1
Lösbarkeit eines Linearen Gleichungssystems mit zwei Gleichungen und zwei Unbekannten |