Lösung von Aufgabe 12.9
Aus Geometrie-Wiki
Version vom 15. Juli 2010, 00:34 Uhr von Heinzvaneugen (Diskussion | Beiträge)
Es gelte der Innenwinkelsatz für Dreiecke. Beweisen Sie den starken Außenwinkelsatz.
Starke Außenwinkelsatz: In jedem Dreieck ist das Maß eines jeden Außenwinkels so groß wie die Summe der Größen der beiden nichtanliegenden Innenwinkel.
Lösung 1
VSS: Dreieck  ,
, 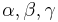 sind Innenwinkel des Dreiecks
sind Innenwinkel des Dreiecks  ,
, 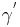 ist Außenwinkel.
ist Außenwinkel.
Es gelte der Satz zur Innenwinkelsumme im Dreieck!
Beh: aBdA: 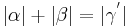
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 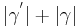 = 180 = 180
|
(Def. Nebenwinkel), (Supplementaxiom) |
| (II) | 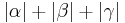 = 180 = 180
|
(Satz Innenwinkelsumme im Dreieck) |
| (III) | 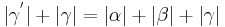
|
(I), (II), (rechnen mit reellen Zahlen) |
| (IV) | 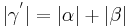
|
(III), (rechnen mit reellen Zahlen) |
--> Beh ist wahr. analoge Beweisführung für 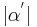 und
und 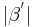 bzgl den entsprechenden nichtanliegenden Innenwinkeln.
bzgl den entsprechenden nichtanliegenden Innenwinkeln.
--Löwenzahn 09:58, 14. Jul. 2010 (UTC)

