Beispiele, Gegenbeispiele
Beispiel 1
Wir gehen von der additiven Gruppe der Restklassen modulo 6 aus ![[\mathbb{Z}_6, \oplus]](/images/math/9/0/d/90daaa2a8d1138539ff15f39a74f58c8.png) . .
Die Gruppe besteht aus den folgenden Restklassen: 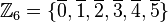
Die Gruppentafel sieht wie folgt aus:
Wir wählen aus  die folgende Teilmenge die folgende Teilmenge 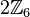 aus: aus:
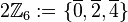
![[2\mathbb{Z}_6, \oplus]](/images/math/e/3/2/e32854e004ab70107710abac0af772d9.png) ist eine Gruppe und damit eine Untergruppe von ist eine Gruppe und damit eine Untergruppe von ![[\mathbb{Z}_6, \oplus]](/images/math/9/0/d/90daaa2a8d1138539ff15f39a74f58c8.png)
Beispiel 2
Die Gruppe der Bewegungen
Die Gruppenmitglieder
Unter einer Bewegung  versteht man eine abstandserhaltende Abbildung der Ebene auf sich: versteht man eine abstandserhaltende Abbildung der Ebene auf sich:
Es sei  unsere Ebene. unsere Ebene.
 ist Relation ist Relation
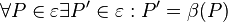
 ist eindeutig und damit Abbildung ist eindeutig und damit Abbildung
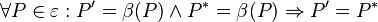
 ist abstandserhaltend ist abstandserhaltend
Die Menge aller Bewegungen wollen wir mit  bezeichnen. bezeichnen.
Die Verknüpfung
wir wählen als Verknüpfung auf 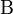 die NAF von Abbildungen und kennzeichnen diese mit die NAF von Abbildungen und kennzeichnen diese mit  . .
![[\Beta, \circ]](/images/math/0/d/b/0dbb39c2e6e24499e8dd3049f199a7df.png) ist Gruppe ist Gruppe
Abgeschlossenheit
Es seien  und und  zwei Bewegungen. zwei Bewegungen.
Wir haben zu zeigen, dass 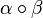 eine Bewegung ist. eine Bewegung ist.
Da die NAF zweier Abbildungen der Ebene auf sich ist tivialerweise wieder eine Abbildung der Ebene auf sich. Wir müssen nur zeigen dass 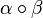 abstandserhaltend ist: abstandserhaltend ist:

Assoziativität
Die NAF von Abbildungen ist immer assoziativ.
Einselement
Wir betrachten die Abbildung 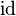 , die jeden Punkt die Abbildung der ebene auf sich selbst abbildet: , die jeden Punkt die Abbildung der ebene auf sich selbst abbildet:
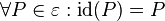
Damit ist 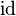 eine Abbildung der Ebene auf sich. Wegen eine Abbildung der Ebene auf sich. Wegen 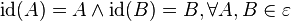 gilt natürlich auch gilt natürlich auch 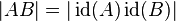 . .
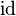 erfüllt die Eigenschaften eines Einselementes: erfüllt die Eigenschaften eines Einselementes:
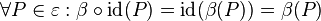 und somit und somit 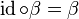 . .
inverse Elemente
Es genügt zu zeigen, dass jede Bewegung  eineindeutig ist, d.h. dass jeder Punkt eineindeutig ist, d.h. dass jeder Punkt 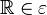 bei bei  ein und nur ein Urbild ein und nur ein Urbild 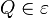 hat. hat.
Injektivität von 
Sei 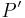 das Bild von das Bild von  bei der Bewegung bei der Bewegung  . Wir haben zu zeigen, dass es keinen Punkt . Wir haben zu zeigen, dass es keinen Punkt 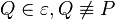 gibt, der durch gibt, der durch  auch auf auch auf 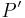 abgebildet wird. Wir nahemen, an, dass es einen solchen Punkt abgebildet wird. Wir nahemen, an, dass es einen solchen Punkt  gibt. Dann gilt: gibt. Dann gilt:
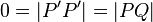 und damit und damit 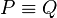 , was ein Widerspruch zur Annahme , was ein Widerspruch zur Annahme 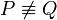 ist. ist.
Surjektivität von 
Wir haben zu zeigen, dass jeder Punkt 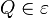 bei der Bewegung bei der Bewegung  ein Urbild hat. ein Urbild hat.
Annahme:  hat kein Urbild bei hat kein Urbild bei  . Da jeder Punkt der Ebene . Da jeder Punkt der Ebene  durch durch  auf genau einen Punkt der Ebene auf genau einen Punkt der Ebene  abgebildet wird und der Punkt abgebildet wird und der Punkt  kein Urbild hat, müssen wenigstens zwei verschiedene Punkte kein Urbild hat, müssen wenigstens zwei verschiedene Punkte  und und  aus aus  durch durch  auf ein und denselben Punkt auf ein und denselben Punkt  abgebildet werden: abgebildet werden:
-
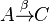
-
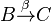
Wegen 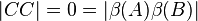 müssen müssen  und und  ein und derselbe Punkt, also identisch sein. Das ist ein Widerspruch zu ein und derselbe Punkt, also identisch sein. Das ist ein Widerspruch zu 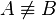 . Unsere Annahme . Unsere Annahme  hat kein Urbild ist also zu verwerfen. hat kein Urbild ist also zu verwerfen.
Die Untergruppe der Drehungen um ein und denselben Punkt
Drehungen
- Eine Bewegung die entweder die Identität ist oder genau einen Fixpunkt
 besitzt, heißt Drehung um besitzt, heißt Drehung um  . .
|