Lösungen zu den Übungsaufgaben der Serie 3 SoSe 2020
Inhaltsverzeichnis |
Aufgabe 3.1
Aufgabe 3.1 a)
Schauen Sie in den Qelltext. Die Tilde ~ muss jeweils ersetzt werden.
Wenn Sie mit der Tabellensyntax nicht klar kommen, schauen Sie sich erst die Aufgabe 3.5 an. Die Tabellen sind kleiner und übersichtlicher und damit schneller zu verstehen.
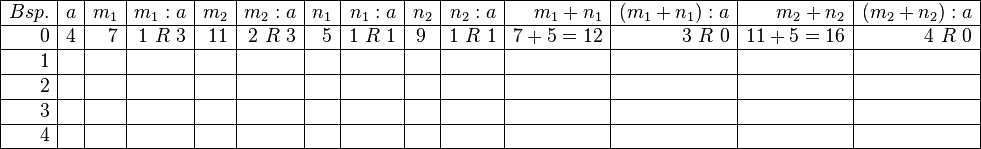
Aufgabe 3.1 b)
Voraussetzung 1
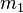 und
und 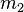 lassen bei Division durch
lassen bei Division durch 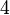 denselben Rest
denselben Rest 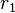 .
.
also:
Voraussetzung 1.1
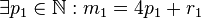
Voraussetzung 1.2
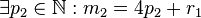
Voraussetzung 2=
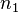 und
und 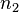 lassen bei Division durch
lassen bei Division durch 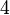 denselben Rest
denselben Rest 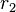 .
.
also:
=Voraussetzung 2.1
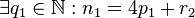
Voraussetzung 2.2

Behauptung
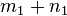 sowie
sowie 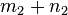 lassen bei Division durch
lassen bei Division durch 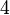 jeweils denselben Rest
jeweils denselben Rest 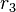 .
.
Oder anders ausgedrückt:
Es sei 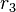 der Rest, der bei der Division von
der Rest, der bei der Division von 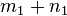 durch
durch 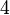 gelassen wird.
gelassen wird.
Behauptung (und damit zu zeigen): 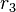 wird auch bei der Division von
wird auch bei der Division von 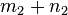 durch
durch 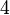 gelassen.
gelassen.
Beweis
Aufgabe 3.1 c)
Voraussetzung 1
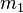 und
und 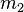 lassen bei Division durch
lassen bei Division durch  denselben Rest
denselben Rest 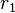 .
.
also:
Voraussetzung 1.1
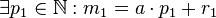
Voraussetzung 1.2
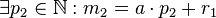
Voraussetzung 2=
also:
=Voraussetzung 2.1
Voraussetzung 2.2
Behauptung
Beweis
Aufgabe 3.2
Aufgabe 3.3
Aufgabe 3.4
Aufgabe 3.5
Aufgabe 3.5 a)
Schauen Sie in den Quelltext. Die Logik der Tabellenbeschreibung sollte sich Ihnen recht schnell erschließen. Ersetzen Sie das Konstrukt \ldots durch die jeweilige Lösung.
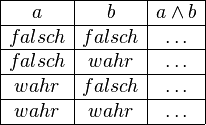
Aufgabe 3.5 b)
Schauen Sie in den Quelltext. Die Logik der Tabellenbeschreibung sollte sich Ihnen recht schnell erschließen. Ersetzen Sie das Konstrukt \ldots durch die jeweilige Lösung.
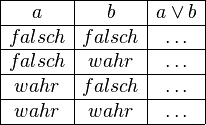
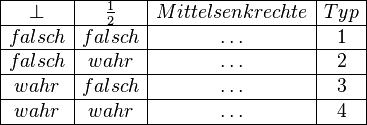
Aufgabe 3.5 c)
Schauen Sie in den Quelltext. Die Logik der Tabellenbeschreibung sollte sich Ihnen recht schnell erschließen. Ersetzen Sie das Konstrukt \ldots durch die jeweilige Lösung.

Aufgabe 3.6
Kleiner Tip: