Lösungen zu den Übungsaufgaben der Serie 3 SoSe 2020
Inhaltsverzeichnis[Verbergen] |
Aufgabe 3.1
Aufgabe 3.1 a)
Schauen Sie in den Qelltext. Die Tilde ~ muss jeweils ersetzt werden.
Wenn Sie mit der Tabellensyntax nicht klar kommen, schauen Sie sich erst die Aufgabe 3.5 an. Die Tabellen sind kleiner und übersichtlicher und damit schneller zu verstehen.
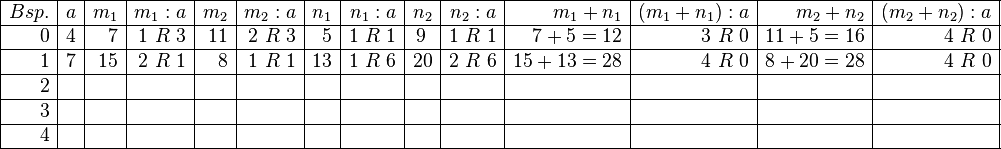
Aufgabe 3.1 b)
Voraussetzung 1
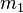 und
und 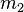 lassen bei Division durch
lassen bei Division durch 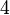 denselben Rest
denselben Rest 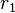 .
.
also:
Voraussetzung 1.1
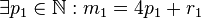
Voraussetzung 1.2
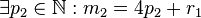
Voraussetzung 2=
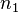 und
und 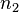 lassen bei Division durch
lassen bei Division durch 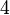 denselben Rest
denselben Rest 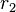 .
.
also:
=Voraussetzung 2.1
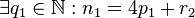
Voraussetzung 2.2

Behauptung
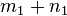 sowie
sowie 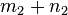 lassen bei Division durch
lassen bei Division durch 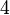 jeweils denselben Rest
jeweils denselben Rest 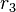 .
.
Oder anders ausgedrückt:
Es sei 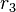 der Rest, der bei der Division von
der Rest, der bei der Division von 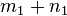 durch
durch 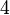 gelassen wird.
gelassen wird.
Behauptung (und damit zu zeigen): 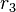 wird auch bei der Division von
wird auch bei der Division von 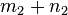 durch
durch 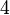 gelassen.
gelassen.
Beweis
[[Datei: ]]Aufgabe 3.1 c)
Voraussetzung 1
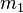 und
und 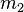 lassen bei Division durch
lassen bei Division durch  denselben Rest
denselben Rest 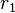 .
.
also:
Voraussetzung 1.1
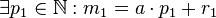
Voraussetzung 1.2
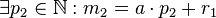
Voraussetzung 2
also:
Voraussetzung 2.1
Voraussetzung 2.2
Behauptung
Beweis
Aufgabe 3.2
[[Datei: ]]Aufgabe 3.2 a)
- Achsensymmetrie 1:
- Achsensymmetrie 2:
- Achsensymmetrie 3:
- Achsensymmetrie 4:
Aufgabe 3.2 b)
- Drehung 1:
- Drehung 2:
- Drehung 3:
- Drehung 4:
Aufgabe 3.2 c)
- (a) gleichzeitig zwei Drehsymmetrien und zwei Achsensymmetrien haben :
- (b) nur Achsensymmetrien haben:
- (c) nur Drehsymmetrien haben:
- (d) genau eine Achsensymmetrie haben:
- (e) genau zwei Achsensymmetrien haben:
- (f) bei folgenden Viereckstypen sind alle Repräsentanten ähnlich zueinander:
Aufgabe 3.2 d)
Schiefdrachen:
Aufgabe 3.2 e)
[[Datei: ]]Drachen
Aufgabe 3.2 f)
Raute unter Verwendung des unmittelbaren Oberbegriffs
Aufgabe 3.2 g)
Haus der Vierecke unter dem Gesichtspunkt Symmetrien: z.B.
- 8 Symmetrien
- 7 Symmetrien
- 6 Symmetrien
- 5 Symmetrien
- 4 Symmetrien
...
Aufgabe 3.3
Aufgabe 3.3 a)
Definition:(Mittelsenkrechte)
- Wenn eine Gerade
 eine Strecke in deren Mittelpunkt in einem rechten Winkel schneidet, so ist diese Gerade die Mittelsenkrechte der Strecke.
eine Strecke in deren Mittelpunkt in einem rechten Winkel schneidet, so ist diese Gerade die Mittelsenkrechte der Strecke.
Aufgabe 3.3 b)
Satz 3.2: (Halbes Mittelsenkrechtenkriterium)
- Es sei
 die Mittelsenkrechte von
die Mittelsenkrechte von  .
.
-
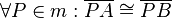 .
.
Formulieren Sie Satz 3.2 in "`Wenn Dann"' ohne die Verwendung von mathematischer Formelsprache.
Wenn ein Punkt  auf der Geraden
auf der Geraden  liegt, dann hat er denselben Abstand zu Punkt
liegt, dann hat er denselben Abstand zu Punkt  wie zu Punkt
wie zu Punkt  .
.
Aufgabe 3.3 c)
Formulieren Sie Satz 3.2 in mathematischer Formelsprache, ohne den Allquantor zu verwenden:
Aufgabe 3.3 d)
Beweis von Satz 3.2
[[Datei: ]]Aufgabe 3.3 e)
Umkehrung von Satz 3.2
Es sei  eine Gerade, die die Strecke
eine Gerade, die die Strecke  schneidet.
schneidet.
Wenn 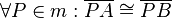 gilt, dann ist m die Mittelsenkrechte der Strecke
gilt, dann ist m die Mittelsenkrechte der Strecke  .
.
Aufgabe 3.3 f)
Äquivalenz, Mittelsenkrechtenkriterium
Aufgabe 3.3 g)
Es sei  eine Implikation. Unter der Kontraposition dieser Implikation versteht man die Implikation
eine Implikation. Unter der Kontraposition dieser Implikation versteht man die Implikation 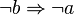 . Formulieren Sie die Kontraposition von Satz 3.2.
. Formulieren Sie die Kontraposition von Satz 3.2.
Aufgabe 3.3 h)
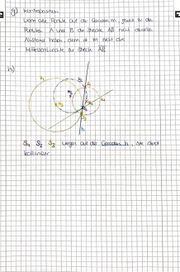
Begründen Sie in der ebenen Geometrie: Es seien 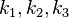 drei Kreise mit den Mittelpunkten
drei Kreise mit den Mittelpunkten 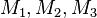 . Wenn der Schnitt aller drei Kreise genau zwei Punkte beinhaltet, dann sind
. Wenn der Schnitt aller drei Kreise genau zwei Punkte beinhaltet, dann sind 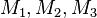 kollinear.
kollinear.
(Googeln Sie ggf. kolinear)
Aufgabe 3.4
Aufgabe 3.4 a)
Definieren Sie den Begriff Drachenviereck über die Diagonaleneigenschaft.
Aufgabe 3.4 b)
Es sei  ein Viereck mit
ein Viereck mit 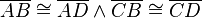 . Beweisen Sie, dass
. Beweisen Sie, dass  ein Drachen ist.
ein Drachen ist.
Aufgabe 3.4 c)
Definieren sie Rauten als spezielle Drachen.
Aufgabe 3.5
Aufgabe 3.5 a)
Schauen Sie in den Quelltext. Die Logik der Tabellenbeschreibung sollte sich Ihnen recht schnell erschließen. Ersetzen Sie das Konstrukt \ldots durch die jeweilige Lösung.

Aufgabe 3.5 b)
Schauen Sie in den Quelltext. Die Logik der Tabellenbeschreibung sollte sich Ihnen recht schnell erschließen. Ersetzen Sie das Konstrukt \ldots durch die jeweilige Lösung.

Aufgabe 3.5 c)
Schauen Sie in den Quelltext. Die Logik der Tabellenbeschreibung sollte sich Ihnen recht schnell erschließen. Ersetzen Sie das Konstrukt \ldots durch die jeweilige Lösung.

Aufgabe 3.6
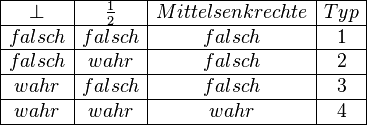
Um ein grundlegendes Verständnis für einen Begriff zu vermitteln, arbeitet man im Mathematikunterricht mit vielen Beispielen und Gegenbeispielen. Für den Begriff "`Mittelsenkrechte"' müssen prinzipiell zwei Bedingungen erfüllt sein: Die Gerade muss senkrecht auf der Strecke stehen 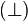 und diese halbieren
und diese halbieren  . Dann und nur dann, wenn die Verknüpfung
. Dann und nur dann, wenn die Verknüpfung  wahr ist, darf die entsprechende Gerade Mittelsenkrechte der jeweiligen Strecke genannt werden. Aus diesem "`und-Konstrukt"' lässt sich eine grundlegende Klassifizierung von Gegenbeispielen bezüglich einer didaktisch wertvollen schulischen Erabeitung des Begriffs Mittelsenkrechte ableiten. Beschreiben Sie diese Klassifizierung.
wahr ist, darf die entsprechende Gerade Mittelsenkrechte der jeweiligen Strecke genannt werden. Aus diesem "`und-Konstrukt"' lässt sich eine grundlegende Klassifizierung von Gegenbeispielen bezüglich einer didaktisch wertvollen schulischen Erabeitung des Begriffs Mittelsenkrechte ableiten. Beschreiben Sie diese Klassifizierung.
Kleiner Tip: