Definitionen von Studenten

Höhe eines Dreiecks

1. Die Höhe hc (oBdA) eines Dreiecks $\overline {ABC}$ ist die Länge des Lotes von C auf AB.
   --Löwenzahn 18:05, 19. Jul. 2010 (UTC)
2. Ich würde eher sagen, dass die Höhe gleich dem Lot ist und die Länge der Höhe gleich der Länge des Lotes. Ich meine: die Höhe ist eine Strecke (die man "einzeichnen" kann), die Länge ist jedoch eine Zahl...
   --"chris"07 18:30, 19. Jul. 2010 (UTC)
3. Aber: ist das Lot die Lotstrecke oder die Lotgerade? Dadurch ist jene Definition, die Höhe sei gleich dem Lot nicht eindeutig zu bejahen. Sicherheitshalber "Lotsrecke" statt "Lot" im ersten Teil der Definition (2), dadurch ergibt sich auch die Identität der Strecken und die Länge muss nicht zusätzlich erwähnt werden.
   --Heinzvaneugen 07:42, 20. Jul. 2010 (UTC)
4. Ok, danke euch. Also dann besser: "Die Höhe hc (oBdA) eines Dreiecks $\overline {ABC}$ ist die Lotstrecke von C auf AB." Dabei muss ich aber nicht mehr sagen, dass die Lotstrecke über die Lotgerade bestimmt ist, oder?
   --Löwenzahn 15:39, 20. Jul. 2010 (UTC)
5. Schau mal im Skript (Höhen eines Dreiecks)...da ist die Höhe dem Lot gleichgesetzt, wenn ich es nicht falsch verstehe, habe dort deswegen auch eine Diskussion eröffnet ;)--"chris"07 19:10, 20. Jul. 2010 (UTC)
6. Idee um dem Problem zu entgehen. Weiß nicht ob es so stimmt. Es sei das Dreieck ABC. L ist der Lotfußpunkt des Lotes durch C auf AB. Die Höhe hc des Dreiecks ABC ist der Abstand von CL.--Frühling 16:30, 21. Jul. 2010 (UTC)

Kommentar: --*m.g.* 18:59, 21. Jul. 2010 (UTC)
Die Höhen eines Dreiecks sind Strecken.

Stufenwinkel

Die folgende Definition wurde uns per mail zugesandt: Sie ist nach meinem Erachten korrekt.--*m.g.* 18:59, 21. Jul. 2010 (UTC) Es seien 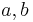$\ a, b$ und $\ c$ 3 komplanare, paarweise verschiedene Geraden, wobei $\ c$ die Geraden $\ a$ und $\ b$ in den zwei Punkten $\ A$ und $\ B$ schneiden möge. Die Winkel $\ \alpha$ und $\ \beta$ , von denen einer $\ A$ und einer $\ B$ als Scheitelpunkt haben möge , heißen Stufenwinkel, wenn ein Schenkel von $\ \alpha$ in derselben Halbebene bzgl. $\ c$ liegt, wie ein Schenkel von $\ \beta$ und wenn ein Schenkel eines der beiden Winkel Teilmenge eines Schenkels des anderen Winkels ist.

Kontraposition

Ich habe mal ne Frage zur Kontraposition. Wenn zb ein Satz heißt: "Aus nicht Zw (A,B,C) folgt nicht Zw (C,B,A)", dann kann ich doch auch die Implikation beweisen, also "Aus Zw (A,B,C) folgt Zw (C,B,A)", oder? Ich habe ja damit dann auch die Kontraposition gezeigt?!?! --Löwenzahn 15:36, 21. Jul. 2010 (UTC)

Was du formuliert hast ist aber nicht die Implikation. Es müsste doch heißen: Aus Zw (C,B,A) folgt Zw (A,B,C). Denn Implikation bedeutet aus a folgt b und die zugehörige Kontraposition ist aus nicht b folgt nicht a.