Definitionen von Studenten

Höhe eines Dreiecks

1. Die Höhe hc (oBdA) eines Dreiecks $\overline {ABC}$ ist die Länge des Lotes von C auf AB.
   --Löwenzahn 18:05, 19. Jul. 2010 (UTC)
2. Ich würde eher sagen, dass die Höhe gleich dem Lot ist und die Länge der Höhe gleich der Länge des Lotes. Ich meine: die Höhe ist eine Strecke (die man "einzeichnen" kann), die Länge ist jedoch eine Zahl...
   --"chris"07 18:30, 19. Jul. 2010 (UTC)
3. Aber: ist das Lot die Lotstrecke oder die Lotgerade? Dadurch ist jene Definition, die Höhe sei gleich dem Lot nicht eindeutig zu bejahen. Sicherheitshalber "Lotsrecke" statt "Lot" im ersten Teil der Definition (2), dadurch ergibt sich auch die Identität der Strecken und die Länge muss nicht zusätzlich erwähnt werden.
   --Heinzvaneugen 07:42, 20. Jul. 2010 (UTC)
4. Ok, danke euch. Also dann besser: "Die Höhe hc (oBdA) eines Dreiecks $\overline {ABC}$ ist die Lotstrecke von C auf AB." Dabei muss ich aber nicht mehr sagen, dass die Lotstrecke über die Lotgerade bestimmt ist, oder?
   --Löwenzahn 15:39, 20. Jul. 2010 (UTC)
5. Schau mal im Skript (Höhen eines Dreiecks)...da ist die Höhe dem Lot gleichgesetzt, wenn ich es nicht falsch verstehe, habe dort deswegen auch eine Diskussion eröffnet ;)--"chris"07 19:10, 20. Jul. 2010 (UTC)
6. Idee um dem Problem zu entgehen. Weiß nicht ob es so stimmt. Es sei das Dreieck ABC. L ist der Lotfußpunkt des Lotes durch C auf AB. Die Höhe hc des Dreiecks ABC ist der Abstand von CL.--Frühling 16:30, 21. Jul. 2010 (UTC)

Kommentar: --*m.g.* 18:59, 21. Jul. 2010 (UTC)
Die Höhen eines Dreiecks sind Strecken. Warum soll die Höhe 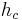$\ h_c$ o.B.d.A. betrachtet werden?

1. @ --Frühling. Ist das mit "Abstand" nicht das gleiche Problem wie mit "Länge", das damit nicht die Strecke, sondern das Maß der Strecke gemeint ist?--Löwenzahn 17:18, 22. Jul. 2010 (UTC)
2. Neuer Versuch (allgemeiner): Eine Höhe eines Dreiecks, ist das Lot eines Eckpunktes des Dreiecks auf eine Gerade, die durch die gegenüberliegende Dreiecksseite bestimmt ist.--Löwenzahn 17:18, 22. Jul. 2010 (UTC)

Stufenwinkel

Die folgende Definition wurde uns per Mail zugesandt: Sie ist nach meinem Erachten korrekt.--*m.g.* 18:59, 21. Jul. 2010 (UTC)
Es seien 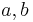$\ a, b$ und $\ c$ 3 komplanare, paarweise verschiedene Geraden, wobei $\ c$ die Geraden $\ a$ und $\ b$ in den zwei Punkten $\ A$ und $\ B$ schneiden möge. Die Winkel $\ \alpha$ und $\ \beta$ , von denen einer $\ A$ und einer $\ B$ als Scheitelpunkt haben möge, heißen Stufenwinkel, wenn ein Schenkel von $\ \alpha$ in derselben Halbebene bzgl. $\ c$ liegt, wie ein Schenkel von $\ \beta$ und wenn ein Schenkel eines der beiden Winkel Teilmenge eines Schenkels des anderen Winkels ist.

Ich bin der Meinung, die Definition ist dann korrekt, wenn mit Halbebene die offene Halbebene gemeint ist. Wenn die geschlossene gemeint ist, müsste es heißen: "wenn $\ \alpha$ und $\ \beta$ in derselben Halbebene bzgl. $\ c$ liegen und wenn ein Schenkel" ... - oder nicht?

--Sternchen 20:40, 22. Jul. 2010 (UTC)

Fehlt an der ersten Definintion nicht, dass a und b parallel zueinander sind? Wie wäre das? Es seien AB und CD zueinander parallele Geraden, die von AC geschnitten werden. Dann wären o.B.d.A. folgende Winkel Stufenwinkel zueinander: AC-, AB+ zu CA+, CD+ --Nicola 12:51, 24. Jul. 2010 (UTC)

Lot von einem Punkt auf eine Gerade

Die folgende Definition wurde uns per Mail zugesandt: Sie ist nach meinem Erachten korrekt.--*m.g.* 19:07, 21. Jul. 2010 (UTC)--*m.g.* 18:59, 21. Jul. 2010 (UTC)
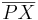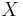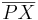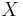Es sei $\ g$ eine Gerade und $\ P$ ein Punkt außerhalb der Geraden $\ g$. Die Strecke $\ \overline{PX}$ nennt man Lot von $\ P$ auf $\ g$, wenn $\ X$ Element von $\ g$ ist und $\ \overline{PX}$ Teilmenge der Senkrechten zu $\ g$ durch $\ X$ ist.

Innenwinkel eines Dreiecks

Die folgende Definition wurde uns per Mail zugesandt: Sie ist nach meinem Erachten fast korrekt (Formulierungsoptimierung!).--*m.g.* 19:12, 21. Jul. 2010 (UTC)
Ein Winkel, dessen Scheitelpunkt Eckpunkt eines Dreicks ist und bei dem für beide Schenkel gilt, dass eine Dreiecksseite Teilmenge eines Schenkels ist, heißen Innenwinkel eines Dreiecks.

Ein Winkel, dessen Scheitelpunkt Eckpunkt eines Dreiecks ist und der zwei verschiedene Dreiecksseiten als Teilmenge hat, heißt Innenwinkel eines Dreiecks.

--Sternchen 20:44, 22. Jul. 2010 (UTC)

Basis eines gleichschenkligen Dreiecks

Die folgende Definition wurde uns per Mail zugesandt: Sie ist ungewöhnlich, aber korrekt. --*m.g.* 19:13, 21. Jul. 2010 (UTC)
Die Dreiecksseite im gleichschenkligen Dreiecks, die mit den beiden zueinander kongruenten Dreiecksseiten jeweils genau einen Punkt gemeinsam hat, heißt Basis des Dreiecks.

Definition Halbkreis

Kommentar --*m.g.* 19:09, 21. Jul. 2010 (UTC): Versuchen Sie es mit einem ganzen Kreis, einer Geraden durch den Mittelpunkt des Kreises und den durch die Gerade bestimmten Halbebenen. Viel Erfolg.

Es sei g eine Gerade durch einen Durchmesser eines Kreises k. Ein (geschlossener) Halbkreis ist die Schnittmenge einer Halbebenen bezüglich g und dem Kreis k.

ODER:
Die Menger aller Punkt des Kreis k, die bezüglich der Geraden g (, die durch ein Durchmesser des Kreises k festgelegt ist,) in ein und der selben Halbebenen liegen, heißt Halbkreis.
--Tja??? 09:34, 23. Jul. 2010 (UTC)

Kontraposition

Ich habe mal ne Frage zur Kontraposition. Wenn zb ein Satz heißt: "Aus nicht Zw (A,B,C) folgt nicht Zw (C,B,A)", dann kann ich doch auch die Implikation beweisen, also "Aus Zw (A,B,C) folgt Zw (C,B,A)", oder? Ich habe ja damit dann auch die Kontraposition gezeigt?!?! --Löwenzahn 15:36, 21. Jul. 2010 (UTC)

Was du formuliert hast ist aber nicht die Implikation. Es müsste doch heißen: Aus Zw (C,B,A) folgt Zw (A,B,C). Denn Implikation bedeutet aus a folgt b und die zugehörige Kontraposition ist aus nicht b folgt nicht a.

Oh, stimmt. Habs falsch eingetippt. Also nochmal: "Aus nicht Zw (A,B,C) folgt nicht Zw (C,B,A)", davon die Kontraposition "Aus Zw (C,B,A) folgt Zw (A,B,C)". Kann ich dann einfach die Kontraposition des Satzes Beweisen und davon ausgehen, dass somit auch die Implikation bewiesen ist? --Löwenzahn 17:12, 22. Jul. 2010 (UTC)

Der Einwand von Frühling ist m.E. nicht so zwingend, wie es aussieht. 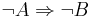$\neg A \Rightarrow \neg B$ kann ja genausogut die Implikation sein, von der man ausgeht. Und davon heißt die Kontraposition dann eben 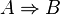$A \Rightarrow B$. Aus Gründen der Verständigung bleibt man gern bei der Implikation 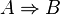$A \Rightarrow B$, das ist natürlich vollkommen richtig. Aber es gibt halt auch Implikationen wie 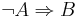$\neg A \Rightarrow B$ und die Kontraposition davon heißt 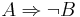$A \Rightarrow \neg B$. Also nichts festlegen, was sich nicht festlegen lässt. Jede Kontraposition ist ja an sich selbst eine Implikation...

Um deine Frage zu beantworten, Löwenzahn: JA! Die Implikation ist in der Logik auf eine bestimmte Art definiert genauso wie Negation und Kontraposition. Und aus diesen Definitonen ergibt sich zwingend, dass eine Implikation und ihre Kontraposition äquivalente Wahrheitswerte haben.

--Sternchen 21:03, 22. Jul. 2010 (UTC)

Punkte für Halbebenen erschaffen

Die folgende Frage wurde uns per Mail zugesandt. Ich beantworte sie hier, weil die Antwort ggf. für weitere Studierende interessant sein könnte.--*m.g.* 19:32, 21. Jul. 2010 (UTC)

Frage:
Wenn ich mir in einem Beweis Punkte "erschaffen" muss (z.B. bei dem Beweis des Satzes "Halbebenen sind konvexe Punktmengen", würde ich mir als Erstes 2 Punkte in Halbebene E1 "schaffen"), mit welcher welcher Begründung kann ich dies tun?? -->Kann ich das Axiom vom Lineal benutzen, wenn ich keinen Strahl habe? -->Kann ich als Begründung Axiom I/3 anführen? -->Dieses Axiom besagt zwar, dass es 3 nicht kollineare Punkte gibt, aber diese müssen ja nicht unbedingt in meiner Halbebene E1 liegen(sie könnten ja auch in E2 liegen) -->Kann ich als Begründung anführen "Ebenen sind Punktmengen? -->Aber eigentlich weiß ich nur sicher, dass eine Ebene 3 Punkte enthält(Satz), nun entsteht doch dasselbe Problem wie bei I/3.

Antwort:
Fall 1: Wir haben nur die ersten beiden Axiomengruppen zur Verfügung.

In diesem Fall verwenden wir den Satz: Jede Ebene enthält wenigstens drei paarweise verschiedene Punkte. (Diese sind letztlich nach der Beweisführung des Satzes sogar nicht kollinear.

Fall 2: Wir haben die ersten drei Axiomengruppen zur Verfügung (Inzidenz, Abstand, Anordnung).

Jede Eben und jede Gerade enthält überabzählbar viele (paarweise) verschiedene Punkte, an denen wir uns wahllos bedienen können.

Sehnenviereck

Wir haben am Freitag bei *m.g.* das Sehnenviereck wie folgt definiert:
Ein Viereck, dessen Seiten Sehnen ein und desselben Kreises k sind, ist ein Sehnenviereck.

Meine Frage:
Kann ich daraus auch die Definition machen: Ein Viereck mit einem Umkreis heißt Sehnenviereck.
Und dann davon ausgehen, dass "Jedes Sehnenviereck einen Umkreis hat", oder müsste man das erst beweisen. Bzw, Frage an die Dozenten: Kann ich in der Klausur davon ausgehen dass wir es bewiesen haben (falls nötig)?--Löwenzahn 11:52, 25. Jul. 2010 (UTC)

"Jedes Sehnenviereck hat einen Umkreis" wäre ja ein Satz, der zu beweißen wäre aus der Definition des Sehnenvierecks heraus, die du gegeben hast mit: "Ein Viereckt mit einem Umkreis heißt Sehnenviereckt." --TimoRR 19:15, 25. Jul. 2010 (UTC)

Absolute Geometrie/ euklidische Geometrie

So ich versuche jetzt mal zuzuordnen welche Sätze zur Absoluten und welche zur eukldischen Geometrie gehören. Bitte ergänzt und verbessert!

Absolute Geometrie: WSW- Kongruenzsatz, SSS- Kongruenzsatz, Basiswinkelsatz und seine Umkehrung, Mittelsenkrechtenkriterium, Existenz und Eindeutigkeit des Lotes, schwacher Außenwinkelsatz, Winkel- Seiten- Beziehung,Satz über Schnittpunkt der Mittelsenkrechten/ Höhen(?), Winkelhalbierendekriterium, Existenz und Eindeutigkeit der Seitenhalbierenden im Dreieck,

nur zur euklidischen Geometrie: Stufenwinkelsatz und seine Umkehrung, Wechselwinkelsatz und seine Umkehrung, Satz über entgegengesetzt liegende Winkel und seine Umkehrung, starker Außenwinkelsatz, Satz über Existenz von Parallelen, Satz über die Innenwinkelsumme im Dreieck, Satz des Thales (+ Umkehrungen), Zentri- Periperiewinkelsatz, Satz über gegenüberliegende Seiten (Winkel oder?) im Sehnenviereck

--Frühling 15:27, 26. Jul. 2010 (UTC)

Korrektur:--Löwenzahn 16:06, 26. Jul. 2010 (UTC) also Umkehrung Stufenwinkelsatz, Wechselwinkelsatz und entgegengesetzt liegende Winkel sind absolute Geometrie, genauso der Satz über die Existenz von Parallelen

Neuer Vorschlag:

Absolute Geometrie:

... → WSW- Kongruenzsatz → SSS- Kongruenzsatz → Basiswinkelsatz und seine Umkehrung → Mittelsenkrechtenkriterium → Existenz und Eindeutigkeit des Lotes → schwacher Außenwinkelsatz → Lemmas + Korollare → gr. Winkel - gr. Seite Beziehung + Umkehrung → Umkehrung Stufenwinkelsatz → Umkehrung Wechselwinkelsatz → Umkehrung Satz über entgegengesetzt liegende Winkel → Satz über Existenz von Parallelen

Nur euklidische Geometrie:

→ Stufenwinkelsatz → Wechselwinkelsatz → Satz über entgegengesetzt liegende Winkel → starker Außenwinkelsatz → Satz über die Innenwinkelsumme im Dreieck → Höhenpktsatz → Satz(Schnittpkt der Mittelsenkrechten eines Dreiecks) → Winkelhalbierendekriterium!? → Existenz und Eindeutigkeit der Seitenhalbierenden im Dreieck (wird mit dem EP begründet!) → Satz(Schnittpkt Seitenhalbierende eines Dreiecks) → Satz über gegenüberliegende Winkel im Sehnenviereck → Satz des Thales + Umkehrungen → Zentri- Periperiewinkelsatz

--Principella 22:15, 27. Jul. 2010 (UTC)

Def gleichschenkliges Trapez

1. Ein Trapez mit einem Umkreis heißt gleichschenkliges Trapez.
2. Ein Trapez mit zwei zueinander nicht gegenüberliegenden Winkel, heißt gleichschenkliges Trapez.
3. Ein Trapez mit zwei zueinander kongruenten Seiten, die nicht parallel sind, heißt gleichschenkliges Trapez.

Bitte um Kommentar--Löwenzahn 07:15, 27. Jul. 2010 (UTC)

zu 2. Ein Trapez in dem jeweils die zwei Winkel kongruent zueinander sind, die an einer der Parallelen anliegen heißt gleichschenkliges Trapez.

4. Ein Trapez das eine Symmetrieachse durch die beiden Mittelpunkte der Parallelen besitzt heißt gleichschenkliges Trapez.--Frühling 11:01, 27. Jul. 2010 (UTC)

Def geschlossene Halbebene

$\ gQ^{-}:= \{P| \exists S\,\{S\}=g\cap\overline {PQ} \}$

So steht es im Wikiskript. Das ist so aber nicht korrekt, oder? Es müsste noch die Gerade g dazu, also: 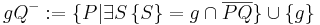$\ gQ^{-}:= \{P| \exists S\,\{S\}=g\cap\overline {PQ} \} \cup \{g\}$

Gänseblümchen 19:00, 27. Jul. 2010 (UTC) _______________________________________________________________________________________________________________________ Def geschlossene Halbebene: 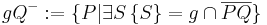$\ gQ^{-}:= \{P| \exists S\,\{S\}=g\cap\overline {PQ} \}$ Ich formuliere es mal mit Worten, damit man es besser versteht: $\ gQ^{-}$ ist die Menge aller Punkte für die gilt: Die Strecke $\overline {PQ}$ und die Trägergerade g haben einen Punkt gemeinsam.

Mit dieser Definition sind alle Punkte inbegriffen, für die diese "Eigenschaft" zutrifft und egal welchen Punkt P der Geraden g ich mit Q verbinde, die entsprechende Strecke $\overline {PQ}$ hat immer einen Schnittpunkt mit g und zwar P selbst. Die "Eigenschaft" trifft also auch zu wenn P auf g liegt. Du kannst die Punkte der geschlossenen Halbebene mit g nochmal vereinigen, am Resultat verändert sich nichts, aber du hattest die Punkte von g mit dieser Definition eigentlich schon dabei... --Principella 20:59, 27. Jul. 2010 (UTC)

Vielen Dank Principella, es ist mir klar geworden, warum ich nicht nochmal mit g vereinigen muss --> Die Ps können ja auch direkt auf der Geraden g liegen, somit gibt es auch einen Schnittpunkt (=Berührpunkt) PQ mit g, damit sind alle Punkte von g auch Element der Halbebene 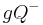$gQ^{-}$ . --Gänseblümchen 21:30, 27. Jul. 2010 (UTC)