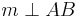Mittelsenkrechte und Winkelhalbierende
Inhaltsverzeichnis |
Mittelsenkrechte und Winkelhalbierende
Mittelsenkrechte
Eine Mittelsenkrechte ist das, was ihre Bezeichnung ausdrückt: eine Gerade, die eine Strecke halbiert und senkrecht auf ihr steht.
Definition VI.1: (Mittelsenkrechte)
- Es sei
 eine Gerade und
eine Gerade und  eine Strecke, die durch
eine Strecke, die durch  im Punkt
im Punkt  geschnitten wird.
geschnitten wird.  ist die Mittelsenkrechte von
ist die Mittelsenkrechte von  , wenn
, wenn
- Es sei
Satz VI.1: (Existenz und Eindeutigkeit der Mittelsenkrechten)
- Jede Strecke hat in jeder Ebene, zu der die Strecke vollständig gehört, genau eine Mittelsenkrechte.
Beweis von Satz VI.1
Es sei  eine Strecke, die vollständig zur Ebene
eine Strecke, die vollständig zur Ebene  gehören möge.
gehören möge.
Behauptungen:
- Es gibt in
 Gerade
Gerade  , die die Mittelsenkrechte von
, die die Mittelsenkrechte von  ist.
ist.
- Es gibt in
 nicht mehr als eine Gerade
nicht mehr als eine Gerade  , die die Mittelsenkrechte von
, die die Mittelsenkrechte von  ist.
ist.
Beweis der Existenzbehauptung:
Aus Gründen der effizienten Bezeichnung führen wir den Punkt  ein, der zur Ebene
ein, der zur Ebene  aber nicht zur Geraden
aber nicht zur Geraden  gehören möge.
gehören möge.
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (i) | 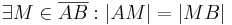
|
Definition III.1 (Mittelpunkt) |
| (ii) | 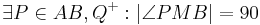
|
Definition V.6 (rechter Winkel) |
| (iii) | 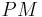 ist Mittelsenkrechte von ist Mittelsenkrechte von 
|
(ii), (i), Definition V.8 (Relation senkrecht), Definition VI.1 (Mittelsenkrechte) |
Bemerkung: Ihnen fällt sicherlich auf, dass wir nach dem Beweis von Satz V.5 die Existenz der Mittelsenkrechten von  gar nicht so ausführlich hätten führen müssen. Der Beweis von Satz V.5 steht momentan jedoch noch als Übungsaufgabe aus.
gar nicht so ausführlich hätten führen müssen. Der Beweis von Satz V.5 steht momentan jedoch noch als Übungsaufgabe aus.
Beweis der Eindeutigkeitsbehauptung
Die Eindeutigkeit des Mittelpunktes einer Strecke wurde bereits bewiesen (Satz III.1). Die Eindeutigkeit der Senkrechten in einem Punkt einer Geraden zu dieser Geraden wird/wurde mit Satz V.5 bewiesen.
Winkelhalbierende
Ein Winkel ist ein Paar von Halbgeraden, die einen gemeinsamen Anfangspunkt haben. Eine Winkelhalbierende teilt einen Winkel in zwei Teilwinkel, die jeweils dieselbe Größe haben. Die Teilwinkel werden dadurch gebildet, dass jeder Schenkel des ursprünglichen Winkels jeweils mit der Winkelhalbierenden zu einem neuen Winkel zusammengefasst wird. Es ist also sinnvoll, die Winkelhalbierende eines Winkels als eine besondere Halbgerade zu definieren.
Definition VI.2
- Es seien
 ,
,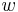 und
und 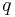 drei Halbgeraden ein und derselben Ebene mit dem gemeinsamen Anfangspunkt
drei Halbgeraden ein und derselben Ebene mit dem gemeinsamen Anfangspunkt  . Die Halbgerade
. Die Halbgerade 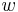 ist die Winkelhalbierende des Winkels
ist die Winkelhalbierende des Winkels 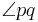 , wenn
, wenn 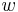 im Inneren von
im Inneren von 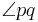 liegt und die beiden Winkel
liegt und die beiden Winkel 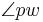 und
und 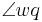 dieselbe Größe haben.
dieselbe Größe haben.
- Es seien
Wenn w identisch zu p oder q wäre, was nach UNSERER Definition "Inneres eines Winkels" durchaus möglich ist, dürfen wir dann trotzdem noch von einer Winkelhalbierenden sprechen? (Die Größe der beiden Winkel 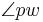 und
und 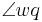 müsste zwar 0 sein, aber sie könnten ja trotzdem noch gleichgroß sein...)
--Principella 23:50, 16. Jul. 2010 (UTC)
müsste zwar 0 sein, aber sie könnten ja trotzdem noch gleichgroß sein...)
--Principella 23:50, 16. Jul. 2010 (UTC)
Satz VI.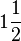
- Es sei
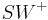 die Winkelhalbierende des Winkels
die Winkelhalbierende des Winkels  . Dann gilt
. Dann gilt 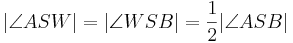 .
.
- Es sei
Beweis von Satz VI.
Übungsaufgabe 10.4
Satz VI.2 (Existenz und Eindeutigkeit der Winkelhalbierenden)
- Zu jedem Winkel gibt es genau eine Winkelhalbierende.
Beweis von Satz VI.2
Übungsaufgabe 10.5
Die Lösung dieser Übungsaufgabe dient der Antwort von 10.4... Doch wo wird Satz V.2 bewiesen: Zu jedem Winkel gibt es GENAU EINE Winkelhalbierende?