Lösung von Aufgabe 12.4
Beweisen Sie die Existenz und die Eindeutigkeit des Lotes von einem Punkt  auf eine Gerade
auf eine Gerade  .
.
Existenz
Voraussetzung: Gerade  , Punkt
, Punkt 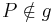
Behauptung: Es existiert ein Lot 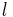 von
von  auf
auf  mit Lotfußpunkt
mit Lotfußpunkt 
Analoge Behauptung (Definition von Lot) Es existiert eine Senkrechte auf  , die durch
, die durch  geht.
geht.
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | Es existiert ein Punkt 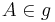 , der Abstand zu P beträgt , der Abstand zu P beträgt 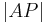
|
Axiom I/1 (Axiom von der Geraden), Axiom III.1 (Axiom vom Lineal) |
| (II) | Am Scheitelpunkt 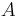 wird an der Gerade wird an der Gerade 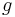 der Winkel der Winkel 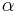 in die Halbebene in die Halbebene 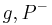 abgetragen. abgetragen.
|
Winkelkonstruktionsaxiom |
| (III) | Auf dem entstanden Strahl trägt man die Länge von 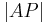 ab. Es entsteht der Punkt ab. Es entsteht der Punkt  . .
|
Axiom III.1 (Axiom vom Lineal) |
| (IV) | 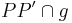 . Der Schnittpunkt sei . Der Schnittpunkt sei  . .
|
 und und  liegen in unterschiedlichen Halbebenen bezogen auf liegen in unterschiedlichen Halbebenen bezogen auf  . .
|
| (V) | Es entstehen zwei kongruente Dreiecke 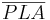 und und 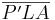
|
SWS
S - |
| (VI) | Die Winkel an  sind rechte Winkel sind rechte Winkel
|
(IV), (V), kongruente Nebenwinkel sind rechte Winkel (Definition V.6 : Rechter Winkel) |
| (VII) | 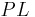 steht senkrecht auf steht senkrecht auf 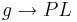 ist Lotgerade, ist Lotgerade, 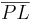 ist Lot(strecke) ist Lot(strecke)
|
(VI), Definition Lot |
Kleine Anmerkung: Bei Schritt (II) muss man an sich auch definieren, dass der Winkel 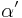 bezüglich
bezüglich 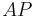 in der selben Halbebene liegt wie
in der selben Halbebene liegt wie 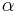 . An dieser Stelle wurde es wg. besserer Übersicht weggelassen.
. An dieser Stelle wurde es wg. besserer Übersicht weggelassen.
Man könnte ja einfach sagen, dass nkoll(P, A, P') gelten soll. Dann wäre der zweite mögliche, für uns jedoch nicht nützliche Winkel ausgeschlossen. --Barbarossa 08:03, 24. Jul. 2010 (UTC)
Eindeutigkeit
Voraussetzung: Gerade  , Punkt
, Punkt 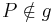 , Lot
, Lot 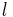 von
von  auf
auf  mit Lotfußpunkt
mit Lotfußpunkt 
Behauptung: Es existiert genau ein Lot von  auf
auf  .
.
Indirekter Beweis - Annahme: Es existieren zwei "Lote" von  auf
auf  .
.
Annahme: Es existiert ein zweiter Lotfußpunkt 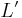
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | Es existiert ein Dreieck 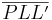
|
VSS, Punkte 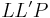 sind nicht kollinear, da sind nicht kollinear, da 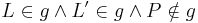 laut Definition Lot und Lotfußpunkt. laut Definition Lot und Lotfußpunkt.
|
| (II) | 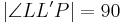
|
Annahme, 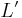 ist Lotfußpunkt ist Lotfußpunkt
|
| (III) | 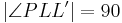
|
VSS,  ist Lotfußpunkt ist Lotfußpunkt
|
| (IV) | Außenwinkel von 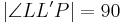
|
Supplementaxiom |
| (V) | 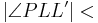 Außenwinkel von Außenwinkel von 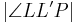
|
Schwacher Außenwinkelsatz |
| (VI) | Annahme muss verworfen werden | Widerspruch zwischen (V) und (III) !!! |
--Heinzvaneugen 00:27, 13. Jul. 2010 (UTC)
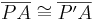 (III)
(III)
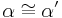 (II)
(II)
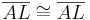 trivial
trivial