Lösung von Aufgabe 12.3
Aufgabenstellung
Beweisen Sie:
Korollar 2 zum schwachen Außenwinkelsatz
- Die Summe der Größen zweier Innenwinkel eines Dreiecks ist stets kleiner als 180.
Lösung 1
Die Beweisführung ist natürlich sehr ähnlich zu Aufgabe 12.2.
Der Einfachheit halber werden die Winkel mit 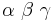 bezeichnet, die jeweiligen Außenwinkel sind dann
bezeichnet, die jeweiligen Außenwinkel sind dann 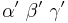 .
.
Voraussetzung: Dreieck 
Behauptung; Die Summe der Größen zweier Innenwinkel eines Dreiecks ist stets kleiner als 180.
Indirekter Beweis. Annahme: Die Summe der Größen zweier Innenwinkel eines Dreiecks kann 180 oder mehr betragen.
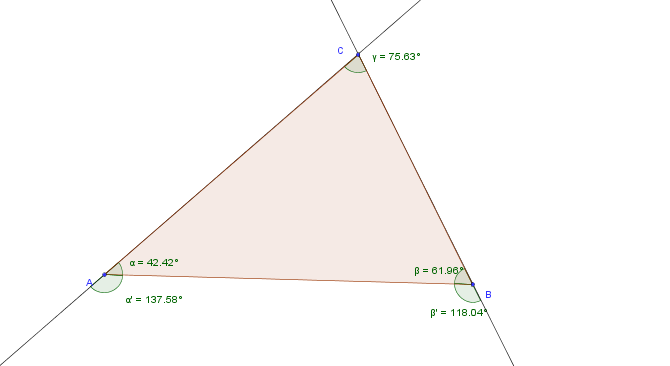
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | Es gilt: 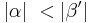 und und 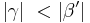
|
schwacher Außenwinkelsatz |
| (II) | 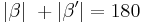
|
Axiom IV.4: (Supplementaxiom): Nebenwinkel sind supplementär. |
| (III) | 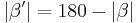
|
(II), Algebraische Umformung |
| (IV) | 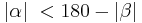 und und 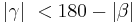
|
(I), (III) |
| (V) | 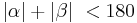 und und 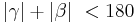
|
(IV), Algebraische Umformung |
| (VI) | Es gilt: 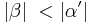 und und 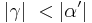
|
schwacher Außenwinkelsatz |
| (VII) | 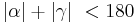 und und 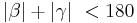
|
Beweis zusammengefasst, analog zu Schritte (I) bis (V) |
Aus (V) und (VII) folgt, dass die Annahme verworfen werden muss.
--Heinzvaneugen 01:55, 12. Jul. 2010 (UTC)
== Lösung 2 ==
Sei ABC ein Dreieck mit den schulüblichen Bezeichnungen. Laut dem schwachen Außenwinkelsatz gilt, dass 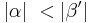 .
.
Zudem gilt wegen Nebenwinkelaxiom und nach Umformung: 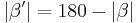 Nun gilt:
Nun gilt: 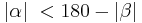 Nach Umformung erhält man:
Nach Umformung erhält man: 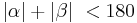 .
.

