Lösung von Aufgabe 1.2 WS2010
Aus Geometrie-Wiki
Version vom 23. Oktober 2010, 13:38 Uhr von Bagheera (Diskussion | Beiträge)
Es seien  drei paarweise verschiedene Punkte mit
drei paarweise verschiedene Punkte mit
(*) 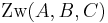 .
.
zu zeigen:
(**) 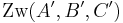
Wir übersetzen zunächst (*):
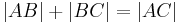
entsprechend (**) haben wir zu zeigen, dass 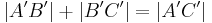 gilt.
gilt.
Den Rest können Sie alleine ... .
Lösungsmöglichkeit 1
| Voraussetzung: | Existenz von A, B, C mit A ungleich B, B ungleich C , C ungleich A und Zw (A, B, C) |
| Behauptung: | 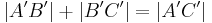
|
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 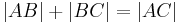
|
Voraussetzung + Def. Zwischenrelation |
| (II) | 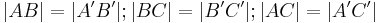
|
(I) + Abstandsinvarianz der Bewegung (Def. Bewegung) |
| (III) | 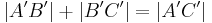
|
(I)+(II) Rechnen mit rationalen Zahlen |
| (IV) | 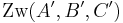
|
(III) + Def. Zwischenrelation |
sehr gut, --*m.g.* 16:10, 20. Okt. 2010 (UTC)
Die Frage mag haarspalterisch sein (sorry), aber warum in Beweisschritt II die Begründung mit (I)? --Bagheera 12:38, 23. Okt. 2010 (UTC)

