Lösung von Aufgabe 1.3 WS2010)
Aus Geometrie-Wiki
Version vom 18. November 2010, 00:29 Uhr von Engel82 (Diskussion | Beiträge)
Es seien 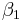 und
und 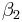 zwei Bewegungen.
zwei Bewegungen.
zu zeigen:
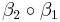 ist eine Bewegung.
ist eine Bewegung.
Lösungidee, noch zu ergänzen!!
Voraussetzung:AB; 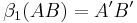 ;
; 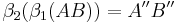
Behauptung:
1. 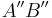 ist Abbild von AB
ist Abbild von AB
2. Abstandsinvarianz
Teil 2:
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 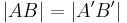
|
Voraussetzung + Def. Bewegung |
| (II) | 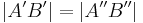
|
Voraussetzung + Def. Bewegung |
| (III) | 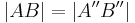
|
(1),(2), Transität der Streckenkongruenz |
| (IV) | 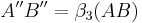
|
(3)+ Def. Bewegung. |
Der Beweis ist vermutlich unvollständig, da noch zu zeigen ist, dass es sich um eine Abbildung handelt. Gezeigt habe ich nur, dass die Abstandsinvarianz gegeben ist.--Tja??? 15:39, 21. Okt. 2010 (UTC)

