Lösung von Aufg. 7.4 (SoSe 11)

Satz I: Je drei nicht kollineare Punkte sind paarweise verschieden.

1. Wir formulieren Satz I neu und beginnen mit „Es seien $A$, $B$ und $C$ drei Punkte.“ Ergänzen Sie: „Wenn $A$,$B$ und $C$ … , dann … .“
2. Beweisen Sie Satz I indirekt.
3. Bilden Sie die Kontraposition von Satz I.
4. Beweisen Sie auch die Kontraposition von Satz I.
5. Formulieren Sie die Umkehrung von Satz I.
6. Gilt auch die Umkehrung von Satz I?

1. Es seien $A$, $B$ und $C$ drei Punkte. Wenn $A$,$B$ und $C$ nicht kollinear sind , dann sind sie paarweise verschieden.

---

2. Beweis:
Voraussetzung: nkoll ($A$, $B$, $C$)
Behauptung: $A$, $B$ und $C$ paarweise verschieden
Annahme (für indirekten Beweis): zwei der drei Punkte sind NICHT verschieden, also identisch, sagen wir mal, o.B.d.A. $A$ und $B$
Aus Axiom I/1 folgt, dass es genau eine Gerade gibt, der $A$ und der dritte Punkt $C$ angehören.
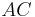Da $A$ aber mit $B$ identisch ist (Annahme), gehört $B$ auch dieser Geraden $AC$ an.
Da es also eine Gerade gibt, der alle drei Punkte angehören, sind sie kollinear, was ein Widerspruch zur Voraussetzung ist.
Das gleiche gilt, wenn ich $B$ und $C$ oder $A$ und $C$ in der Annahme identisch setze. Ich habe das Gefühl, hier viele Schritte gemacht zu haben, die gar nicht notwendig sind - und auch beim nächsten bin ich mir unsicher, ob der überhaupt gebraucht wird: Falls $A$, $B$ und $C$ identisch sind, kann ich einen vierten Punkt wählen, durch den und die drei identischen eine Gerade legen und schon wieder gibt es eine Gerade, die alle drei Punkte enthält und damit einen Widerspruch zur Voraussetzung erzeugt.

---

3. Kontraposition: Es seien $A$, $B$ und $C$ drei Punkte. Wenn $A$, $B$ und $C$ nicht paarweise verschieden sind , dann sind sie kollinear.
keine Zeit für 4., gleich kommen die Simpsons ;-), ist aber doch im Grunde der Widerspruchsbeweis von oben, oder?
5. Umkehrung: Es seien $A$, $B$ und $C$ drei Punkte. Wenn $A$,$B$ und $C$ paarweise verschieden sind, dann sind sie nicht kollinear.
6. Nein, gilt nicht: drei verschiedene Punkte auf einer Geraden sind das Gegenbeispiel --WikiNutzer 20:26, 24. Mai 2011 (CEST)