Diskussion:Äquivalenzrelationen und Klasseneinteilungen SoSe 11
Diskussion zur Definition der Klasseneinteilung
Definition: (Klasseneinteilung eine Menge)
- Es sei
 eine Menge und
eine Menge und 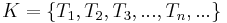 eine Menge von Teilmengen von
eine Menge von Teilmengen von  .
.
 ist eine Klasseneinteilung von
ist eine Klasseneinteilung von  , wenn
, wenn
- Es sei
- notwendige Bedingung 1: Jedes a Element M ist nur in einer Teilmenge von K enthalten (ich weiß leider nicht wo die ganzen kleinen math. Zeichen wie "Element" oder so sind)
- notwendige Bedingung 2: Wieder mit Worten: Die Mächtigkeit jeder Teilmenge
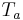
 K ist größer null
K ist größer null
- notwendige Bedingung 3: Die Menge K muss echte Teilmenge von M sein, ansonsten wäre K = M und somit keine Klasseneinteilung
--HecklF 21:47, 25. Apr. 2011 (CEST)
mh, weitere Vorschläge, Änderungen...--Tutorin Anne 21:55, 25. Apr. 2011 (CEST)
Ist Punkt 3 nicht falsch (bzw. da es eine Definition ist nicht sinnvoll) ? müsste es nicht heißen:
Die Vereinigungsmenge von 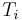 = M ( i = 1, 2, 3,.., n, ...)
--Peterpummel 20:24, 7. Mai 2011 (CEST)
= M ( i = 1, 2, 3,.., n, ...)
--Peterpummel 20:24, 7. Mai 2011 (CEST)
Bemerkung --*m.g.* 15:56, 12. Mai 2011 (CEST):
- Sie haben recht, Bedingung 3 ist so nicht korrekt, allerdings aus dem Grunde, dass wir die Menge selbst nicht als Klasseneinteilung von sich selbst ausschließen dürfen. Also nehmen wir als Klasseneinteilung einer Menge
 nur
nur  selbst, so handelt es sich um eine echte Klasseneinteilung. Das ist vielleicht nicht besonders sinnvoll, wäre jedoch völlig korrekt.
selbst, so handelt es sich um eine echte Klasseneinteilung. Das ist vielleicht nicht besonders sinnvoll, wäre jedoch völlig korrekt.
- Sie haben recht, Bedingung 3 ist so nicht korrekt, allerdings aus dem Grunde, dass wir die Menge selbst nicht als Klasseneinteilung von sich selbst ausschließen dürfen. Also nehmen wir als Klasseneinteilung einer Menge
Ich muss hier leider widersprechen: Punkt 3 ist nicht korrekt da:
I) Um es mit einem Beispiel zu verdeutlichen. Sei M = { 1, 2, 3, 4}, T_1 = { 1, 2}, T_2 = { 3, 4} => K = { {1, 2}, {3, 4}}
Wie soll nun K eine Teilmenge (ob echt oder nicht) von M sein? Ein Element von M ist eine Zahl, die Elemente von K sind Mengen von Zahlen. Dies widerspricht der Definition von "Teilmenge sein", da kein Element von K ein Element von M ist.
II) Mir fehlt bei der obigen Definition das Verständnis von Punkt 3, da gänzlich fehlt, dass die Vereinigung der einzelen Klassen wieder die Menge M ergeben muss.
Das eine Menge M als Klasseneinteilung von sich selbst aufgefasst werden kann ist vielleicht nicht immer sinnig, aber vollkommen nachvollziehbar ( das war auch nicht mein Kritikpunkt) und widerspricht auch nicht der Vorlesung.
--Peterpummel 18:54, 17. Mai 2011 (CEST)

