Diskussion:Äquivalenzrelationen und Klasseneinteilungen SoSe 11
Diskussion zur Definition der Klasseneinteilung
Die alte Diskussion von der Seite
Definition: (Klasseneinteilung eine Menge)
- Es sei
 eine Menge und
eine Menge und 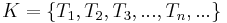 eine Menge von Teilmengen von
eine Menge von Teilmengen von  .
.
 ist eine Klasseneinteilung von
ist eine Klasseneinteilung von  , wenn
, wenn
- Es sei
- notwendige Bedingung 1: Jedes a Element M ist nur in einer Teilmenge von K enthalten (ich weiß leider nicht wo die ganzen kleinen math. Zeichen wie "Element" oder so sind)
- notwendige Bedingung 2: Wieder mit Worten: Die Mächtigkeit jeder Teilmenge
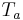
 K ist größer null
K ist größer null
- notwendige Bedingung 3: Die Menge K muss echte Teilmenge von M sein, ansonsten wäre K = M und somit keine Klasseneinteilung
--HecklF 21:47, 25. Apr. 2011 (CEST)
mh, weitere Vorschläge, Änderungen...--Tutorin Anne 21:55, 25. Apr. 2011 (CEST)
Ist Punkt 3 nicht falsch (bzw. da es eine Definition ist nicht sinnvoll) ? müsste es nicht heißen:
Die Vereinigungsmenge von 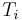 = M ( i = 1, 2, 3,.., n, ...)
--Peterpummel 20:24, 7. Mai 2011 (CEST)
= M ( i = 1, 2, 3,.., n, ...)
--Peterpummel 20:24, 7. Mai 2011 (CEST)
Bemerkung --*m.g.* 15:56, 12. Mai 2011 (CEST):
- Sie haben recht, Bedingung 3 ist so nicht korrekt, allerdings aus dem Grunde, dass wir die Menge selbst nicht als Klasseneinteilung von sich selbst ausschließen dürfen. Also nehmen wir als Klasseneinteilung einer Menge
 nur
nur  selbst, so handelt es sich um eine echte Klasseneinteilung. Das ist vielleicht nicht besonders sinnvoll, wäre jedoch völlig korrekt.
selbst, so handelt es sich um eine echte Klasseneinteilung. Das ist vielleicht nicht besonders sinnvoll, wäre jedoch völlig korrekt.
- Sie haben recht, Bedingung 3 ist so nicht korrekt, allerdings aus dem Grunde, dass wir die Menge selbst nicht als Klasseneinteilung von sich selbst ausschließen dürfen. Also nehmen wir als Klasseneinteilung einer Menge
Ich muss hier leider widersprechen: Punkt 3 ist nicht korrekt da:
I) Um es mit einem Beispiel zu verdeutlichen. Sei M = { 1, 2, 3, 4}, T_1 = { 1, 2}, T_2 = { 3, 4} => K = { {1, 2}, {3, 4}}
Wie soll nun K eine Teilmenge (ob echt oder nicht) von M sein? Ein Element von M ist eine Zahl, die Elemente von K sind Mengen von Zahlen. Dies widerspricht der Definition von "Teilmenge sein", da kein Element von K ein Element von M ist.
II) Mir fehlt bei der obigen Definition das Verständnis von Punkt 3, da gänzlich fehlt, dass die Vereinigung der einzelen Klassen wieder die Menge M ergeben muss.
Das eine Menge M als Klasseneinteilung von sich selbst aufgefasst werden kann ist vielleicht nicht immer sinnig, aber vollkommen nachvollziehbar ( das war auch nicht mein Kritikpunkt) und widerspricht auch nicht der Vorlesung.
--Peterpummel 18:54, 17. Mai 2011 (CEST)
Weitere Bemerkungen zur Diskussion --*m.g.* 23:01, 31. Mai 2011 (CEST)
Punkt 1 und Punkt 2 waren nicht strittig und sind so auch korrekt. Für meine Augen und Ohren ein wenig ungewöhnlich formuliert, was jedoch der Korrektheit der Formulierungen keinen Abbruch tut. Ich finde es im übrigen absolut Klasse, wenn Sie ihre eigenen Formulierungen wählen, da geht dem Dozenten das Herz über.
Punkt 3 muss zum Inhalt haben, dass alle Teilmengen, die zu 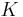 gehören, zusammen die Ausgangsmenge
gehören, zusammen die Ausgangsmenge  bilden.
Das wird durch die Formulierung "Die Menge K muss echte Teilmenge von M sein" nicht korrekt widergespiegelt.
bilden.
Das wird durch die Formulierung "Die Menge K muss echte Teilmenge von M sein" nicht korrekt widergespiegelt.
Der Nebensatz "ansonsten wäre K = M und somit keine Klasseneinteilung" hätte in der Definition auch dann nichts verloren, wenn er und die Definition korrekt wären, denn er erläutert warum die Definition so gewählt wurde. Das darf man in nachgestellten Betrachtungen tun. Zur eigentlichen Definition gehören solche Betrachtungen nicht. (Jetzt bin ich natürlich päpstlicher als der Papst und werde mir gleich wegen eines Verhaltens, das wiederum ein wenig zu lachs ist, selbst eins auf die Mütze hauen müssen.
Zu der Formulierung "ansonsten wäre K = M und somit keine Klasseneinteilung".
Diese bedeutet: Wenn 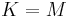 dann ist
dann ist 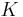 keine Klasseneinteilung von
keine Klasseneinteilung von  .
.
Jetzt wird es schwer:
 ist eine Teilmenge von sich selbst. Definiert man nun die Menge
ist eine Teilmenge von sich selbst. Definiert man nun die Menge 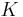 , die ja aus lauter Teilmengen von
, die ja aus lauter Teilmengen von  besteht derart, dass sie lediglich aus der Menge
besteht derart, dass sie lediglich aus der Menge  besteht, dann ist
besteht, dann ist 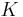 eine korrekte Klasseneinteilung von
eine korrekte Klasseneinteilung von  :
:
(1) Da 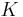 nur aus einer einzigen Teilmenge von
nur aus einer einzigen Teilmenge von  besteht, gilt der Schnitt zweier verschiedener Teilmengen von
besteht, gilt der Schnitt zweier verschiedener Teilmengen von  aus
aus 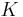 ist leer. Oder wie oben ausgedrückt: Jedes
ist leer. Oder wie oben ausgedrückt: Jedes 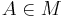 gehört nur zu einer Teilmenge aus
gehört nur zu einer Teilmenge aus 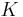 nämlich zu
nämlich zu  .
.
(2) 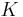 besteht nur aus
besteht nur aus  und damit gehört die leere Menge nicht zu
und damit gehört die leere Menge nicht zu 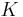 .
.
(3) Die Vereinigungsmenge aller Mengen aus 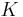 ist
ist  . Da
. Da 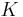 nur aus
nur aus  besteht stimmt das.
Den obigen Sachverhalt habe ich in meiner Bemerkung vom 12. Mai dann nicht ganz korrekt so formuliert: Also nehmen wir als Klasseneinteilung einer Menge
besteht stimmt das.
Den obigen Sachverhalt habe ich in meiner Bemerkung vom 12. Mai dann nicht ganz korrekt so formuliert: Also nehmen wir als Klasseneinteilung einer Menge  nur
nur  selbst, so handelt es sich um eine echte Klasseneinteilung. Diese Formulierung sollte die obigen Überlegungen (1) bis (3) zusammenfassen.
selbst, so handelt es sich um eine echte Klasseneinteilung. Diese Formulierung sollte die obigen Überlegungen (1) bis (3) zusammenfassen.
Korrekterweise muss ich jetzt aber einen Fehler bezüglich der Exaktheit meiner Formulierung eingestehen. (Dank dem Studenten, der mich heute in der Sprechstunde darauf hinwies.):
Korrekterweise darf man nicht formulieren, dass eine Menge von sich selbst eine Klasseneinteilung sein kann. Also 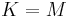 kann nie gelten, denn
kann nie gelten, denn 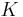 ist eine Menge höherer Ordnung als
ist eine Menge höherer Ordnung als  . Ein Beispiel macht das verständlicher. Es möge gelten
. Ein Beispiel macht das verständlicher. Es möge gelten 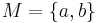 Als Menge aller Teilmengen von
Als Menge aller Teilmengen von  die dann eine Klasseneinteilung von
die dann eine Klasseneinteilung von  sein soll wählen wir die Menge
sein soll wählen wir die Menge 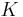 , die nur aus der Menge
, die nur aus der Menge  bestehen möge:
bestehen möge: 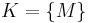 , also
, also 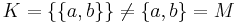 . Alles klar?
. Alles klar?
Vielen Dank für die sehr ausführliche Erläuterung--Peterpummel 13:35, 1. Jun. 2011 (CEST)

