Tangentenkriterium

Tangentenkriterium

Kriterium: (Tangete am Kreis)

Eine Gerade t, die durch einen Punkt A eines Kreises k mit dem Mittelpunkt M verläuft, ist genau dann Tangente an k, wenn t senkrecht auf MA steht.

Satz 1: (Tangete am Kreis)

$\ t \cap k = \lbrace A\rbrace \Rightarrow MA \perp \ t$

Beweis durch Wiederspruch:
Voraussetzung: $\ t \cap k = \lbrace A\rbrace$
Behauptung: 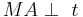$MA \perp \ t$

Annahme: 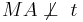$\ MA \not\perp \ t$

1	Es existiert ein Lot von M auf t, dieses ist eindeutig. Der Lotfußpunkt auf k heiße B.	Ex. und Eindeutigkeit Lot, Annahme, Voraussetzung
2	CB| = |BA|	Axiom vom Lineal, Abstandsaxiom, Definition zwischenrelation, Voraussetzung, (1) und Skizze
3	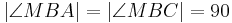$|\angle MBA | = |\angle MBC| = 90$	nach Konstruktion, Def. NW, Def. supplementär, Supplementaxiom, Def. Lot (1)
4	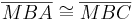$\overline{MBA} \cong \overline{MBC}$	MB| = |MB|
5	MC| = |MA| = r nach Voraussetzung und es ergeben sich zwei Schnittpunkte, was ein Widerspruch zur Voraussetzung ist.

Satz 2: (Tangente am Kreis)

$MA \perp \ t \wedge k \cap t = \lbrace A\rbrace \Rightarrow$
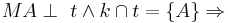
t ist Tangente an k.