12)
Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: 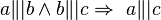 .
.
b) Welche Eigenschaft der Relation  auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
a) Vor.: a,b,c sind paarweise verschiedene Geraden Annahme: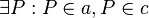
| 1 | Fehler beim Parsen(Unbekannte Funktion „\c“): \ a \|| b \c | Vor. |
| 2 | Fehler beim Parsen(Unbekannte Funktion „\c“): \ b \|| c \c | Vor. |
| 3 | 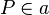 |
Beh. |
| 4 | 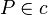 |
Beh. |
| 5 |  |
3,4 ; Widerspruch zur Vorraussetzung |
--Todah raba 20:07, 4. Nov. 2011 (CET)
b) Transitivität --Todah raba 20:07, 4. Nov. 2011 (CET)
Gebe dir in allem recht, würde nur sagen, dass es Aufgrund der Augabenstellung Sinn macht bei dem Beweis den Schritt 5 eher so zu formulieren:
| 5 | 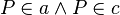 |
3,4 ; Widerspruch zum Parallelaxionom, Durch jeden Punkt kann nur eine Gerade gehen welche Parallel zu b ist. |
Bei der Annahme eventuell noch ergänzen, dass es sich beim dem Punkt P um den Schnittpunkt der beiden Geraden a und c handelt, von welchen wir ja annehmen, dass die nicht parallel sind und somit diesen Schnittpunkt haben müssen.--RicRic 18:13, 5. Nov. 2011 (CET)
@RicRic Meine Vorrausetzung ist doch, dass die Geraden a, b, c paarweise verschieden sind. Wenn ich in meiner Annahme davon ausgehe, dass P sowohl Element der Geraden a als auch der Geraden c ist, dann ist doch die einzige Möglichkeit, dass der Punkt P ein Schnittpunkt der Geraden a und c ist, oder? Muss ich es dann noch zusätzlich ergänzen? --Todah raba 18:23, 6. Nov. 2011 (CET)

