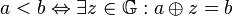Größenbereiche
Inhaltsverzeichnis |
Beispiele
Masse
Wir betrachten physikalische Körper. Jeder Körper hat die Eigenschaft einer Krafteinwirkung Widerstand entgegenzusetzen. Man nennt diese Eigenschaft die träge Masse.
Alle Körper ziehen sich aufgrund ihrer Masse an. Diese Eigenschaft der Körper einander anzuziehen nennt man schwere Masse.
Schwere und träge Masse sind auf das engste miteinander verbunden. Besonders schwere Körper (Körper die andere besonders stark anziehen) sind auch besonders träge.
Die Masse eines Körpers wird dadurch bestimmt, dass man den Körper mit anderen Körpern vergleicht:
[ www.ph-heidelberg.de is not an authorized iframe site ]
Letztlich definieren wir auf der Menge 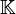 aller Körper eine Relation gleich schwer:
aller Körper eine Relation gleich schwer:
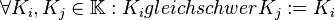 und
und 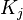 halten sich auf der Waage das Gleichgewicht.
halten sich auf der Waage das Gleichgewicht.
Gewicht
Auf jeden Körper wirkt die Anziehungskraft der Erde. Dies Kraft wird auch Gewichtskraft bzw Gewicht des Körpers genannt. Das Gewicht wird mit einem Federkraftmesser bestimmt. Auf der Menge aller Körper definieren wir: Zwei Körper haben dasselbe Gewicht, wenn sie auf den Federkraftmesser dieselbe Wirkung haben.
Längen
Wir gehen davon aus, dass der Begriff "deckungsgleich" bereits definiert wurde:
Zwei Strecken haben die selbe Länge, wenn sie deckungsgleich sind.--Löwenzahn 16:18, 17. Nov. 2011 (CET)
Flächeninhalte
Wir gehen davon aus, dass der Begriff "zerlegungsgleich" bereits definiert wurde.
Zwei Flächen haben den selben Flächeninhalt, wenn die Flächen zerlegungsgleich sind.--Löwenzahn 16:23, 17. Nov. 2011 (CET)
Volumina
Wie gehen davon aus, dass verdrängen bereits definiert wurde. Zwei Körper haben das selbe Volumen, wenn sie die gleiche Masse an Wasser verdrängen.
Frage: Ist Masse in diesem Zusammenhang korrekt?--Gänseblümchen 17:09, 24. Nov. 2011 (CET)
Geld/Preise
Größen als Äquivalenzklassen
Größen sind Äquivalenzklassen von Objekten:
Z.B.ist die Relation gleichschwer auf der Menge aller Körper eine Äquivalenzrelation:
- Jeder Körper ist zu sich selbst gleichschwer
- Wenn
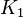 gleichschwer
gleichschwer 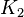 dann ist auch
dann ist auch 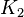 gleichschwer
gleichschwer 
- Wenn
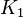 gleichschwer
gleichschwer 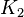 und
und 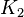 gleichschwer
gleichschwer 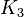 dann
dann 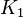 gleichschwer
gleichschwer 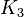
Die Größe Masse ist eine Äquivalenzklasse nach der Äquivalenzrelation gleichschwer.
Hinsichtlich der Größen lassen sich drei Begriffsebenen unterscheiden:
- Repräsentantenebene
- KLassenebene
- Maßzahl ggf. mit Maßeinheit
Vergleichen von Größen
Größen lassen sich vergleichen:
Die Repräsentanten der Klasse 1 sind jeweils kleiner als die Repräsentanten der Klasse 2.
Auf der Menge der Äquivalenzklassen wurde eine Ordnungsrelation definiert. Ordnungsrelationen sind
- irreflexiv
- asymmetrisch
- transitiv
Sind Ordnungsrelationen nicht eigentlich
- reflexiv (
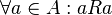 , wobei A eine beliebige Menge sei),
, wobei A eine beliebige Menge sei),
- antisymmetrisch (
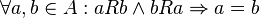 )und
)und
- transitiv (
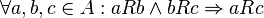 )
)
oder gehe ich fehl? --Flo60 12:41, 13. Nov. 2011 (CET)
Verschiedene Autoren definieren die Begriffe Halbordnung, Ordnung etc. unterschiedlich. Für unsere hier anzustellenden didaktischen Überlegungen sind diese Definitionen nicht so wirklich relevant. Da die Wikipedia Ordnungsrelationen als Verallgemeinerungen der kleiner-gleich Beziehung definiert schließen wir uns dieser Idee hier an und fordern die Antisymmetrie. --*m.g.* 13:24, 17. Nov. 2011 (CET)
Addition von Größen
Beispiel Addition zweier Längen:
Es seien  und
und  zwei Strecken.
zwei Strecken. 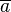 und
und 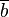 seien die Äquivalenzklassen von
seien die Äquivalenzklassen von  bzw.
bzw.  bezüglich der Relation gleichlang auf der Menge aller Strecken.
Wir addieren
bezüglich der Relation gleichlang auf der Menge aller Strecken.
Wir addieren 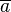 und
und 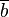 indem wir einen Repräsentanten
indem wir einen Repräsentanten 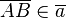 und einen Repräsentanten
und einen Repräsentanten 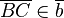 derart auswählen, dass
derart auswählen, dass 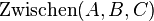 gilt. Die Summe der Längen
gilt. Die Summe der Längen 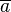 und
und 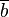 ist dann die Äquivalenzklasse
ist dann die Äquivalenzklasse 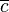 bezüglich der Relation gleichlang, zu der die Strecke
bezüglich der Relation gleichlang, zu der die Strecke 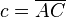 gehört.
gehört.
Allgemeine Defition für Addition von Größen:
Zwei Größen werden addiert, in dem man zwei Repräsentanten für die Größen vereinigt.
z.B.:
Zwei Größe des Geldwertes werden addiert, in dem man die Menge von Münzen und Scheinen zusammenlegt.
Wäre das auch möglich, oder ist das zu allgemein?--Löwenzahn 16:35, 17. Nov. 2011 (CET)
Kommensurabilität und Inkommensurabilität von Größen und Mengen
Wenn eine Menge oder eine Größe messbar ist, indem man Einheitsgrößen zusammenfasst, dann ist diese Menge bzw. Größe kommensurabel. Wenn dies nicht der Fall ist, dann ist sie inkommensurabel.
Beispiel für eine kommensurable Größe: Geldwerte
Wir nehmen an, wir haben einen Geldwert i. H. v. 7,59 €. Mittels unserer Münzen und Scheine kann ich diesen Wert legen. Das tolle ist - und jetzt kommt endlich mal eine gute Nachricht zum Thema Euro (es gab ja fast nur schlechte in letzter Zeit) - es spielt überhaupt keine Rolle, ob es sich um griechische, deutsche, italienische, spanische, französische oder sonstirgendwelche Euros handelt; es funktioniert :-)
Für alle Euroskeptiker unter euch/ihnen, hier ein Photo, um zu zeigen, dass obige Aussage korrekt ist (vielleicht trägt es ja auch dazu bei, dass die Stimmung an den Geldmärkten wieder besser wird):

Inkommensurable Mengen sind demgegenüber Größen und Mengen, welche sich eben nicht durch Einheitsgrößen zusammenfassen lassen. Ein Beispiel hierfür ist die Länge der Diagonale des Einheitsquadrats 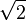 - man kann noch so keine 'Stückchen' aneinanderlegen - die genaue Länge kriegt man nie hin. Ein weiteres Beispiel sind Benzinpreise, welche durch Beträge wie 1,599 (z. B. ein Liter Super) nicht mit unseren Münzen und Scheinen exakt bezahlt werden können. Hier wird gerundet.
- man kann noch so keine 'Stückchen' aneinanderlegen - die genaue Länge kriegt man nie hin. Ein weiteres Beispiel sind Benzinpreise, welche durch Beträge wie 1,599 (z. B. ein Liter Super) nicht mit unseren Münzen und Scheinen exakt bezahlt werden können. Hier wird gerundet.
--Flo60 22:28, 13. Nov. 2011 (CET)
Die mathematische Abstraktion: Größenbereiche
Die Mathematiker abstrahieren den physikalischen Größenbegriff und definieren:
- Es sei
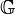 eine nichtleere Menge, auf der eine innere Verknüpfung
eine nichtleere Menge, auf der eine innere Verknüpfung  und eine Ordnungsrelation
und eine Ordnungsrelation 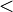 definiert sind. Die Struktur
definiert sind. Die Struktur 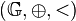 wird Größenbereich genannt, wenn für alle
wird Größenbereich genannt, wenn für alle 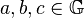 gilt:
gilt:
- Es sei
-
 ist assoziativ auf
ist assoziativ auf 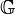 :
: 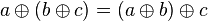
-
 ist kommutativ auf
ist kommutativ auf 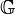 :
: 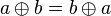
- Für die Relation
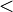 gilt die Trichotomie: Es gilt genau einer der folgenden drei Fälle:
gilt die Trichotomie: Es gilt genau einer der folgenden drei Fälle: 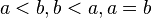
- Für das Zusammenspiel von innerer Verknüpfung
 und der Ordnungsrelation
und der Ordnungsrelation 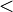 gilt das Lösbarkeitsgesetz:
gilt das Lösbarkeitsgesetz: