12)
Es seien A und B zwei verschiedene Punkte. Welche Ergebnisse erzielen Sie nach den folgenden Mengenoperationen?
a) 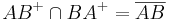
b) 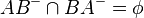
c)  geschnitten mit dem Kreis um
geschnitten mit dem Kreis um  durch
durch  = Den Punkt
= Den Punkt  und den Punkt
und den Punkt 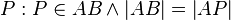
d)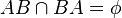
--RicRic 17:52, 6. Dez. 2011 (CET)
a b c scheinen mir logisch,
aber müsste bei d als lösung nicht ab richtig sein, denn ba/ab ist doch die gleiche gerade, oder?
--LouStick 22:28, 6. Dez. 2011 (CET)
Interanter Gedanke! Was meinen die Anderen?--Tutorin Anne 15:38, 7. Dez. 2011 (CET)
Also ich hätte bei d auch gesagt es sind die gleichen Geraden, denn zu zwei Punkten gibt es genau eine Gerade und es sind ja die gleichen Punkte, oder?
Meine Lösung wäre dann alle Punkte Element AB.--Lindi 88 18:23, 7. Dez. 2011 (CET)
Ich dachte auch an AB als Lösung, da ja AB und BA die gleiche Gerade darstellen müssten.
Ich habe noch eine Frage zu c):
Ein Kreis ist doch durch den Mittelpunkt definiert und alle Punkte die von M den gleichen Abstand haben. Wenn eine Gerade den Kreis schneidet, der durch A und B geht, dann ist die Schnittmenge doch eigentlich  und
und  und noch ein weitere Punkt, der zu A den gleichen Abstand hat wie zu B und auf der Geraden liegt? --Cmhock 11:03, 8. Dez. 2011 (CET)
und noch ein weitere Punkt, der zu A den gleichen Abstand hat wie zu B und auf der Geraden liegt? --Cmhock 11:03, 8. Dez. 2011 (CET)

