12)
Aus Geometrie-Wiki
Version vom 8. Dezember 2011, 23:15 Uhr von RicRic (Diskussion | Beiträge)
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
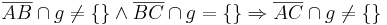
Vor.: 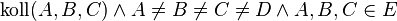
Beh.: 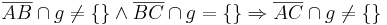
Beweis:
| Schritt | Begründung |
|---|---|
(1)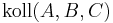 |
Vorr |
(2)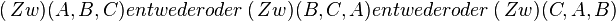 |
Dreiecksungleichung, Abstand kann nicht negativ sein |
(3)Fall 1: 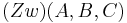 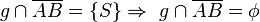 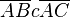 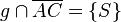 Behaupt stimmt Behaupt stimmt |
verschiedene Geraden haben höchstens einen Punkt gemeinsam, zw Relation, Teilmengenbezieung |
Fall 2: 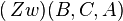 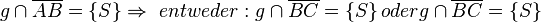 Wiederspruch zur Behauptung | |
Fall 3: 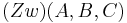 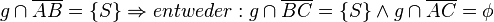 oder: g \cap \overline{AC}=\left\{ {S} \right\} \wedge g \cap \overline{BC}=\phi</math> oder: g \cap \overline{AC}=\left\{ {S} \right\} \wedge g \cap \overline{BC}=\phi</math>
| |
(4)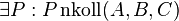 |
A I/3 |
(5) 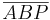 |
AI/1 |
(6) 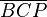 |
AI/1 |
(7) 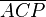 |
AI/1 |
(8) Fall 1: 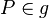 betrachte ich nachher betrachte ich nachher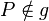 |
|
(9) 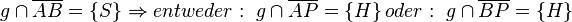 |
Axiom von Pasch ,(5) |
(10) 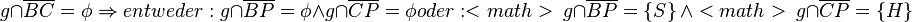 |
Axiom von Pasch ,(6) |
(11) 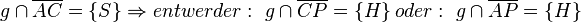 |
Axiom von Pasch ,(7) |
(12)  |
(3) |
(13) 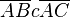 |
(12) |
(14) 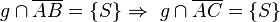 |
(9),10),(11),(13) |
Fall 2 von (7) analog nur mit 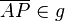
|

