Lösung von Aufgabe 10.4P (SoSe 13)
Beweisen Sie Satz IX.3:
Bei einer Punktspiegelung ist der Schnittpunkt S der beiden Spiegelgeraden a und b Mittelpunkt der Strecke 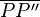 , mit
, mit 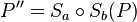 .
.
Voraussetzung:
a ∩ b = {S} ∧ a ⊥ b --Nolessonlearned 18:24, 13. Jul. 2013 (CEST)
Behauptung:
S ist Mittelpunkt von P͞,P͞``
mit P``= Sa∘Sb(P) --Nolessonlearned 18:24, 13. Jul. 2013 (CEST)
Beweis von Nolessonlearnd
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | ∃m: m ∩ a ∩ b = {S}
mit m ≠ a,b |
Voraussetzung;
Konstruktion der Gerade m |
| 2) | Es existiert Q Element von m: Q͞P kongruent Q͞P͞`` | (1); Mittelsenkrechtenkriterium |
| 3) | m senkrecht P͞P͞`` | (2); Def. Mittelsenkrechte |
| 4) | PS| = |SP'| | (3); Mittelsenkrechtenkriterium |
| 5) | S ist Mittelpunkt von P͞P͞`` | (1); (2); (3); (4); Voraussetzung |
Kreative Beweisidee. Zwei Probleme fallen mir auf:
1. Du kannst nicht erst die GErade m konstruieren (dann ist sie bereits fest) und sie dann später als Mittelsenkrechte deuten. (Schritt 2 und 3) - > Diese Schwierigkeit lässt sich leicht beheben.
2. Du kannst nicht in Schritt 5 sagen, dass S Mittelpunkt von PP´´ ist, da dafür laut Def. Mittelpunkt zwei Dinge erfüllt sein müssen: 1. 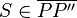 und
und 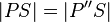 . Ersteres hast du noch nicht gezeigt. --Tutorin Anne 14:04, 16. Jul. 2013 (CEST)
. Ersteres hast du noch nicht gezeigt. --Tutorin Anne 14:04, 16. Jul. 2013 (CEST)
Neuer Versuch
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | 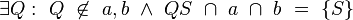
|
Voraussetzung; Konstruktion der Gerade QS |
| 2) | 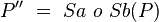
|
Eigenschaft der Punktspiegelung |
| 3) | Fehler beim Parsen(Lexikalischer Fehler): \left| QP \right| \ =\ \left| QP" \right| | (1); (2); Mittelsenkrechtenkriterium |
| 4) | Fehler beim Parsen(Lexikalischer Fehler): \left\{ {S} \right\}\ =\ QS\ \cap\ \overline{PP"} \ \wedge\ QS\ \perp \ \overline{PP"} | (1); (2); (3); Def. Mittelsenkrechte |
| 5) | Fehler beim Parsen(Lexikalischer Fehler): \left| PP" \right|\ =\ \left| PS \right|\ +\ \left| SP" \right| | Def. Zwischen; Eigenschaft der Mittelsenkrechte |
| 6) | Fehler beim Parsen(Lexikalischer Fehler): S\ ist\ Mittelpunkt\ von\ \overline{PP"} | 3); (4); (5) |
Das löst das Problem leider nicht: Du nennst in Schritt 1 einen Punkt Q, damit liegt dieser fest. Erst in Schritt 3 nennst du, dass er zu P und P´´ den gleichen Abstand hat. Hat er aber - wenn nicht zufällig so gezeichnet - gar nicht. Geht echt nicht. --Tutorin Anne 20:06, 17. Jul. 2013 (CEST)
Voraussetzung: Sa∘Sb mit a ∩ b = {S} ∧ a ⊥ b
Behauptung: S ist Mittelpunkt von P͞P"
.
Beweis:
1) Sa∘Sb(P) = P"
Begründung: Eigenschaft d. PS; Voraussetzung
2) Sa∘Sb(S) = S" = S
Begründung: Eigenschaft d. PS; Voraussetzung; S ist Fixpunkt
2b) Drehe a⊥b so, dass P ∈ a und S fest
Begründung: (2); Eigenschaft d. Drehung
3) |PS| + |SP"| = |PP"| mit koll(P,S,P")
Begründung: (1); (2); (2b); Def. Zwischen
4) |PS| = |SP"|
Begründung: (3); Streckentreue d. GS
5) S ist Mittelpunkt von P͞P"
Begründung: (3); (4); Def. Mittelpunkt
--Nolessonlearned 13:26, 18. Jul. 2013 (CEST)
- Der Beweis sieht korrekt aus, ist es aber nicht. Denn Schritt 3 kannst du nicht aus den vorrigen Schritten oder aus der Zwischenrelation herleiten. Du kannst also nicht begründen, dass die Punkte kollinear sind. Dazu musst du das Achsenkreuz drehen, wie es unten im Beweis Schritt 1 entspricht. Dann est kann begründet weden, dass die Punkte kollinear sind. Und wie? --Tutorin Anne 21:09, 18. Jul. 2013 (CEST)
- Ok, ich verstehe. Wüstenfuchs hat die Spiegelachse a verwendet. Ist elegant und schnell. Könnte man theoretisch eine weitere Gerade einfügen, welche die Punkte P,S,P(zweistrich) enthält und diese zur Beweisführung verwenden?--Nolessonlearned 22:10, 18. Jul. 2013 (CEST)
- Nein, das geht nicht. Nur bei der Gerade b weiß ich, dass es eine Fixgerade bezüglich Spiegelung an a ist (da a senkrecht b) und P deshalb wieder auf die GErade gespiegelt wird. Bei allen anderen Geraden weiß ich das nicht. --Tutorin Anne 11:03, 19. Jul. 2013 (CEST)
- Ich dachte, dass bei einer Punktspiegelung jede Gerade, die durch S verläuft eine Fixgerade ist. Diese wäre doch dann ebenfalls für die Beweisführung geeignet. --Nolessonlearned 11:46, 19. Jul. 2013 (CEST)
- Da hast du absolut recht, aber eben genau das soll in diesem Beweis gezeigt werden. --Tutorin Anne 12:24, 19. Jul. 2013 (CEST)
- OK--Nolessonlearned 12:34, 19. Jul. 2013 (CEST)
- OK--Nolessonlearned 12:34, 19. Jul. 2013 (CEST)
- Da hast du absolut recht, aber eben genau das soll in diesem Beweis gezeigt werden. --Tutorin Anne 12:24, 19. Jul. 2013 (CEST)
- Ich dachte, dass bei einer Punktspiegelung jede Gerade, die durch S verläuft eine Fixgerade ist. Diese wäre doch dann ebenfalls für die Beweisführung geeignet. --Nolessonlearned 11:46, 19. Jul. 2013 (CEST)
- Nein, das geht nicht. Nur bei der Gerade b weiß ich, dass es eine Fixgerade bezüglich Spiegelung an a ist (da a senkrecht b) und P deshalb wieder auf die GErade gespiegelt wird. Bei allen anderen Geraden weiß ich das nicht. --Tutorin Anne 11:03, 19. Jul. 2013 (CEST)
Beweis von Wüstenfuchs
| Voraussetzung | a⊥b ∧ a∩b = {S} ∧ Sa∘Sb(P)= P`` |
| Behauptung | IPSI = ISP``I (das ist nicht die komplette Behauptung; s.Anmerkung oben.) |
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | Drehe a⊥b so das P  a und S fest a und S fest |
Vor. ; |
| 2 | Sa(P) = P' = P | 1.) ; Def. Geradenspiegelung |
| 3 | Sb(P') = P`` mit P``  a a |
2.) ; a ist Fixgerade bezüglich der 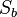
|
| 4 | IPSI = ISP``I | 3.) ; Def. Geradenspiegelung |
| 4b | 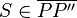 |
... |
| 5 | 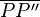 |
4.)+4b) ; Def. Mittelpunkt |
--Wüstenfuchs 20:42, 15. Jul. 2013 (CEST)
Der Beweis ist fast korrekt. Auch hier fehlt die Begründung, dass S auch Element der Strecke PP´´ ist, weil er nur dann Mittelpunkt von PP`` ist. Optimalerweise dafür noch ein Extraschritt einbauen, oder aber die Begründung in 5) ergänzen. --Tutorin Anne 14:13, 16. Jul. 2013 (CEST)

