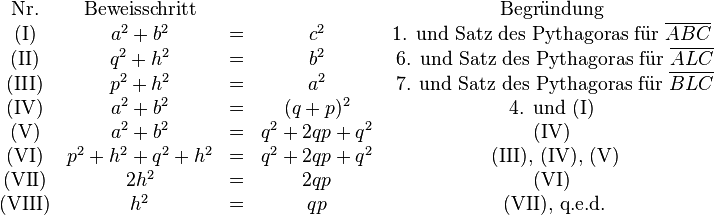Aufgabe 2.8 SoSe 2018
Der Höhensatz für rechtwinklige Dreiecke lautet:
Satz: (Höhensatz)
- In jedem rechtwinkligen Dreieck ist der Flächeninhalt des Quadrates über der Höhe
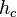 auf die Hypotenuse so groß, wie der Flächeninhalt des Rechtecks, dessen Seitenlängen den Hypotenusenabschnitten auf die Hypotenuse so groß, wie der Flächeninhalt des Rechtecks, dessen Seitenlängen den Hypotenusenabschnitten 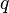 und und  entsprechen. entsprechen.
Kurz: 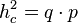
Beweisen Sie den Höhensatz unter Verwendung des Satzes von Pythagoras.
Lösung
- Es sei
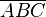 ein rechtwinkliges Dreieck mit dem rechten Winkel ein rechtwinkliges Dreieck mit dem rechten Winkel 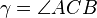 . .
- Die Höhe
 von von  auf die Seite auf die Seite 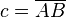 habe auf habe auf  den Fußpunkt den Fußpunkt 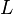 . .
-
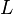 teilt die Hypotenuse teilt die Hypotenuse  in die beiden Hypotenusenabschnitte in die beiden Hypotenusenabschnitte 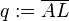 und und 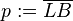 . .
- Es gilt also
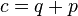 . .
- Weil die Höhe
 senkrecht auf der Hypotenuse senkrecht auf der Hypotenuse  steht, entstehen die zwei rechtwinklige Teildreiecke steht, entstehen die zwei rechtwinklige Teildreiecke 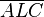 und und 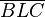 . .
- Im rechtwinkligen Teildreieck
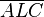 ist ist 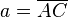 die Hypotenuse und die Hypotenuse und 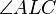 der rechte Winkel. der rechte Winkel.
- Im rechtwinkligen Teildreieck
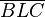 ist ist 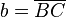 die Hypotenuse und die Hypotenuse und 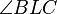 der rechte Winkel. der rechte Winkel.
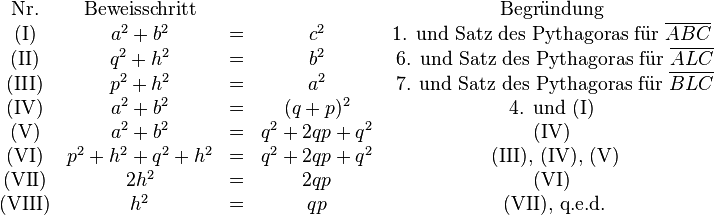
|
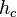 auf die Hypotenuse so groß, wie der Flächeninhalt des Rechtecks, dessen Seitenlängen den Hypotenusenabschnitten
auf die Hypotenuse so groß, wie der Flächeninhalt des Rechtecks, dessen Seitenlängen den Hypotenusenabschnitten 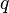 und
und  entsprechen.
entsprechen. 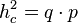
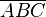 ein rechtwinkliges Dreieck mit dem rechten Winkel
ein rechtwinkliges Dreieck mit dem rechten Winkel 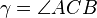 .
.
 von
von  auf die Seite
auf die Seite 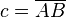 habe auf
habe auf  den Fußpunkt
den Fußpunkt 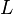 .
.
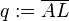 und
und 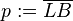 .
.
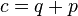 .
.
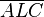 und
und 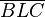 .
.
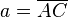 die Hypotenuse und
die Hypotenuse und 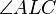 der rechte Winkel.
der rechte Winkel.
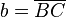 die Hypotenuse und
die Hypotenuse und 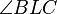 der rechte Winkel.
der rechte Winkel.