Mittelsenkrechte und Winkelhalbierende (SoSe 12)
Mittelsenkrechte und WinkelhalbierendeMittelsenkrechteEine Mittelsenkrechte ist das, was ihre Bezeichnung ausdrückt: eine Gerade, die eine Strecke halbiert und senkrecht auf ihr steht. Erarbeitung der DefinitionMittelsenkrechte, Classroompresenter-Folien aus der Vorlesung vom 21.06.12 Konstruktion der Mittelsenkrechten mittels GeogebraKonstruieren Sie in der folgenden App die Mittelsenkrechte von Definition VI.1: (Mittelsenkrechte)
Satz VI.1: (Existenz und Eindeutigkeit der Mittelsenkrechten)
Beweis von Satz VI.1Die Existenz und Eindeutigkeit des Mittelpunktes einer Strecke wurde bereits bewiesen (Satz III.1). Die Existenz und Eindeutigkeit der Senkrechten in einem Punkt einer Geraden zu dieser Geraden wird/wurde mit Satz V.5 bewiesen. Somit ist Satz VI.1 ebenfalls bewiesen. WinkelhalbierendeEin Winkel ist ein Paar von Halbgeraden, die einen gemeinsamen Anfangspunkt haben. Eine Winkelhalbierende teilt einen Winkel in zwei Teilwinkel, die jeweils dieselbe Größe haben. Die Teilwinkel werden dadurch gebildet, dass jeder Schenkel des ursprünglichen Winkels jeweils mit der Winkelhalbierenden zu einem neuen Winkel zusammengefasst wird. Es ist also sinnvoll, die Winkelhalbierende eines Winkels als eine besondere Halbgerade zu definieren.
Definition VI.2
Satz VI.
|

 eine Gerade und
eine Gerade und  geschnitten wird.
geschnitten wird. 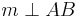

 ,
,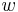 und
und 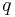 drei Halbgeraden ein und derselben Ebene mit dem gemeinsamen Anfangspunkt
drei Halbgeraden ein und derselben Ebene mit dem gemeinsamen Anfangspunkt  . Die Halbgerade
. Die Halbgerade 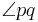 , wenn
, wenn 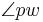 und
und 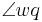 dieselbe Größe haben.
dieselbe Größe haben.
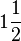
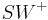 die Winkelhalbierende des Winkels
die Winkelhalbierende des Winkels  . Dann gilt
. Dann gilt 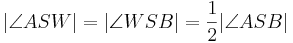 .
.

