Übung Aufgaben 2 S (SoSe 12): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „=Aufgaben zu Sätzen und Beweisen= ==Aufgabe 2.1== Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.<br /> a) Wi…“) |
HecklF (Diskussion | Beiträge) (→Aufgabe 2.7) |
||
| (12 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | =Aufgaben zu Sätzen und Beweisen= | + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> |
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | | valign="top" | | ||
| + | |||
| + | |||
| + | |||
| + | =Aufgaben zu Sätzen und Beweisen Teil 1= | ||
==Aufgabe 2.1== | ==Aufgabe 2.1== | ||
Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.<br /> | Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.<br /> | ||
| Zeile 8: | Zeile 14: | ||
==Aufgabe 2.2== | ==Aufgabe 2.2== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).<br /> | a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).<br /> | ||
b) Es seien ''a'' und ''b'' zwei nichtidentische Geraden, die durch eine dritte Gerade ''c'' jeweils in genau einem Punkt ''S'' geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel <math>\alpha </math> und <math>\beta </math>. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?<br /> | b) Es seien ''a'' und ''b'' zwei nichtidentische Geraden, die durch eine dritte Gerade ''c'' jeweils in genau einem Punkt ''S'' geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel <math>\alpha </math> und <math>\beta </math>. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?<br /> | ||
| Zeile 34: | Zeile 20: | ||
#<math>\|\alpha \|\not= \| \beta \| \Rightarrow \exists S: S \in a \wedge S \in b </math> | #<math>\|\alpha \|\not= \| \beta \| \Rightarrow \exists S: S \in a \wedge S \in b </math> | ||
#<math>\ a \ \|| \ b \Leftrightarrow \alpha \tilde {=} \beta </math> | #<math>\ a \ \|| \ b \Leftrightarrow \alpha \tilde {=} \beta </math> | ||
| + | [[Lösung von Aufgabe 2.2_S (SoSe_12)]] | ||
| + | |||
| + | |||
| + | ==Aufgabe 2.3== | ||
| + | Es seien A und B zwei Punktmengen. Was müssen Sie konkret zeigen, wenn Sie beweisen wollen, dass A = B ?<br /> | ||
| + | |||
[[Lösung von Aufgabe 2.3_S (SoSe_12)]] | [[Lösung von Aufgabe 2.3_S (SoSe_12)]] | ||
==Aufgabe 2.4== | ==Aufgabe 2.4== | ||
| − | + | Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander. <br /> | |
| − | a) | + | |
| − | b) | + | a) Formulieren Sie den Satz mit "Wenn... dann..."<br /> |
| − | [[Lösung von Aufgabe 2.4_S (SoSe_12)]] | + | |
| + | b)Ergänzen Sie:<br /> | ||
| + | Voraussetzung: <math>\overline{ABC} </math> ist ein Dreieck mit…<br /> | ||
| + | Behauptung: | ||
| + | <br /> | ||
| + | [[Lösung von Aufgabe 2.4_S (SoSe_12)]]<br /> | ||
==Aufgabe 2.5== | ==Aufgabe 2.5== | ||
| − | + | Eine Raute sei folgendermaßen definiert: Ein Viereck mit vier kongruenten Seiten heißt Raute. <br /> | |
| + | Sie wollen folgenden Satz beweisen: In einer Raute sind die gegenüberliegenden Seiten parallel zueinander. <br /> | ||
| − | + | a) Formulieren Sie den Satz mit "Wenn... dann..."<br /> | |
| + | b)Ergänzen Sie:<br /> | ||
| + | Voraussetzung: <br /> | ||
| + | Behauptung:<br /> | ||
| + | [[Lösung von Aufgabe 2.5_S (SoSe_12)]]<br /> | ||
==Aufgabe 2.6== | ==Aufgabe 2.6== | ||
| − | + | Bringen Sie die folgenden Implikationen in die Form ''Wenn-Dann'': | |
| − | + | # Jedes Quadrat hat vier rechte Innenwinkel. | |
| − | + | # Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt auf der Hypotenuse dieses Dreiecks. | |
| − | + | # In einem konvexen Viereck schneiden sich die Diagonalen des Vierecks. | |
| − | + | # Die Geraden, die durch die Diagonalen einer Raute <math>\overline{ABCD}</math>eindeutig bestimmt sind, sind Symmetrieachsen von <math>\overline{ABCD}</math>. | |
| − | + | # Es sei <math>\overline{PQRS}</math> ein Paralellogramm. Es gilt: <math>\angle SPQ \tilde= \angle QRS </math>. | |
| − | [[Lösung von Aufgabe 2.6_S (SoSe_12)]] | + | # Die Innenwinkelsumme im Dreieck beträgt 180°. |
| − | + | [[Lösung von Aufgabe 2.6_S (SoSe_12)]]<br /> | |
| + | ==Aufgabe 2.7== | ||
| + | Bilden Sie die Umkehrungen der Implikationen aus Aufgabe 2.6. Formulieren Sie in den Fällen in denen es sinnvoll ist, Implikation und Umkehrung als Äquivalenz.<br /> | ||
| + | [[Lösung von Aufgabe 2.7_S (SoSe_12)]]<br /> | ||
| + | [[Ideen Aufgabe 2.6 mit 2.7 Übung Heckl (SoSe_12)]]<br /> | ||
| + | |} | ||
| + | </div> | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
Aktuelle Version vom 2. Mai 2012, 13:05 Uhr
|
Aufgaben zu Sätzen und Beweisen Teil 1Aufgabe 2.1Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander. Aufgabe 2.2a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach). Lösung von Aufgabe 2.2_S (SoSe_12)
Aufgabe 2.3Es seien A und B zwei Punktmengen. Was müssen Sie konkret zeigen, wenn Sie beweisen wollen, dass A = B ? Lösung von Aufgabe 2.3_S (SoSe_12) Aufgabe 2.4Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander. a) Formulieren Sie den Satz mit "Wenn... dann..." b)Ergänzen Sie: Aufgabe 2.5Eine Raute sei folgendermaßen definiert: Ein Viereck mit vier kongruenten Seiten heißt Raute. a) Formulieren Sie den Satz mit "Wenn... dann..." b)Ergänzen Sie: Aufgabe 2.6Bringen Sie die folgenden Implikationen in die Form Wenn-Dann:
Lösung von Aufgabe 2.6_S (SoSe_12) Aufgabe 2.7Bilden Sie die Umkehrungen der Implikationen aus Aufgabe 2.6. Formulieren Sie in den Fällen in denen es sinnvoll ist, Implikation und Umkehrung als Äquivalenz. |
 und
und  . Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?
. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?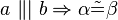
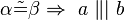
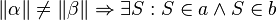
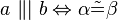
 ist ein Dreieck mit…
ist ein Dreieck mit… eindeutig bestimmt sind, sind Symmetrieachsen von
eindeutig bestimmt sind, sind Symmetrieachsen von 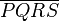 ein Paralellogramm. Es gilt:
ein Paralellogramm. Es gilt: 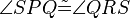 .
.

