Ideen Aufgabe 2.6 mit 2.7 Übung Heckl (SoSe 12)

Aufgabe 2.6

Bringen Sie die folgenden Implikationen in die Form Wenn-Dann.

Aufgabe 2.7

Bilden Sie die Umkehrungen der Implikationen aus Aufgabe 2.6. Formulieren Sie in den Fällen in denen es sinnvoll ist, Implikation und Umkehrung als Äquivalenz.

Ideen

1. Jedes Quadrat hat vier rechte Innenwinkel.

Implikation: Wenn ein Viereck ein Quadrat ist, dann hat es vier rechte Innenwinkel.
Umkehrung:Wenn ein Viereck vier rechte Innenwinkel hat, dann ist es ein Quadrat.

Äquivalenz: GEGENBEISPIEL: RECHTECK.

2. Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt auf der Hypotenuse dieses Dreiecks.

Implikation: Wenn ein Dreieck ein rechtwinkliges ist, dann liegt der Mittelpunkt seines Umkreises auf der Hypotenuse.
Umkehrung: Wenn der Mittelpunkt des Umkreises eines Dreiecks auf einer Seite dieses Dreiecks liegt, dann ist das Dreieck ein rechtwinkliges.
Äquivalenz: Genau dann wenn der Mittelpunkt des Umkreises eines Dreiecks auf einer Seite dieses Dreiecks liegt, dann ist das Dreieck ein rechtwinkliges.

3. In einem konvexen Viereck schneiden sich die Diagonalen des Vierecks.

Implikation: Wenn ein Viereck ein konvexes Viereck ist, dann schneiden sich die Diagonalen dieses Vierecks.
Umkehrung: Wenn sich die Diagonalen eines Vierecks schneide, so ist dieses Viereck ein konvexes Viereck.
Äquivalenz: Genau dann wenn sich die Diagonalen eines Vierecks schneiden, dann ist dieses Viereck ein konvexes Viereck.

4. Die Geraden, die durch die Diagonalen einer Raute $\overline{ABCD}$eindeutig bestimmt sind, sind Symmetrieachsen von $\overline{ABCD}$.

Implikation:
Umkehrung:
Äquivalenz:

5. Es sei $\overline{PQRS}$ ein Paralellogramm. Es gilt: $\angle SPQ \tilde= \angle QRS$.

Implikation:Wenn ein Viereck ein Paralellogramm ist, dann sind die gegenüberliegenden Winkel gleich groß.--Oz44oz 22:08, 2. Mai 2012 (CEST)
Umkehrung: Wenn in einem Viereck die gegenüberliegenden Winkel gleich groß sind, dann ist es ein Paralellogramm.--Oz44oz 22:14, 2. Mai 2012 (CEST)
Äquivalenz: GEGENBEISPIEL: RECHTECK.
Ist ein Rechteck nicht auch ein Parallelogramm?
Guter Gedanke - ein Rechteck ist natürlich auch ein Parallelogramm. Findet sich zur Umkehrung ein adäquates Gegenbeispiel? --Flo60 18:57, 3. Mai 2012 (CEST)

Neuer Versuch:

Implikation:Wenn ein Viereck 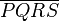$\overline{PQRS}$ ein Paralellogramm ist, dann gilt : $\angle SPQ \tilde= \angle QRS$ .

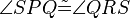Umkehrung: Wenn in einem Viereck 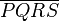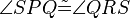$\overline{PQRS}$ $\angle SPQ \tilde= \angle QRS$ gilt, dann ist das Viereck 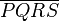$\overline{PQRS}$ ein Paralellogramm.

Äquivalenz: GEGENBEISPIEL: SYM.DRACHE --Oz44oz 18:51, 4. Mai 2012 (CEST)

6. Die Innenwinkelsumme im Dreieck beträgt 180°.

Implikation: Wenn ein Vieleck ein Dreieck ist, dann beträgt die Innenwinkelsumme 180.
Umkehrung: Wenn in einem Vieleck die Innenwinkelsumme 180 beträgt, dann ist das Vieleck ein Dreieck.
Äquivalenz: Genau dann wenn in einem Vieleck die Innenwinkelsumme 180 beträgt, dann ist dieses Vieleck ein Dreieck. --Oz44oz 18:43, 9. Mai 2012 (CEST)
passt --Flo60 20:02, 9. Mai 2012 (CEST)

Zurück zu vorheriger Seite

Übung Aufgaben 2 S (SoSe 12)