Basiswinkelsatz und Mittelsenkrechtenkriterium (SoSe 12): Unterschied zwischen den Versionen
| (9 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> | ||
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | | valign="top" | | ||
| + | |||
| + | |||
| + | |||
== Der Basiswinkelsatz == | == Der Basiswinkelsatz == | ||
=== Gleichschenklige Dreiecke === | === Gleichschenklige Dreiecke === | ||
| Zeile 9: | Zeile 15: | ||
===== Satz VII.5: Basiswinkelsatz ===== | ===== Satz VII.5: Basiswinkelsatz ===== | ||
::In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander. | ::In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander. | ||
| − | + | [[Schulvariante des Beweises des Basiswinkelsatzes]] | |
| − | + | ||
| − | + | ||
| − | [[ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
===== Ein im Rahmen unserer Theorie korrekter Beweis des Basiswinkelsatzes ===== | ===== Ein im Rahmen unserer Theorie korrekter Beweis des Basiswinkelsatzes ===== | ||
Probieren Sie ruhig weitere Varianten: Mittelsenkrechte ... . | Probieren Sie ruhig weitere Varianten: Mittelsenkrechte ... . | ||
| − | Letztlich hilft nur die Winkelhalbierende | + | Letztlich hilft nur die Winkelhalbierende des Winkels, der der Basis des gleichschenkligen Dreiecks gegenüberliegt. Die Winkelhalbierende muss dann die Basis des Dreiecks schneiden. Diese unmittelbar einsichtige Tatsache muss eigentlich bwiesen werden. Wir verweisen diesbezüglich auf die [[Lemmata zu Winkeln]]. |
| − | + | ||
| − | + | ||
| − | + | ||
| + | Hinweis: Im folgenden Beweis berufen wir uns auf Lemma 1. Korrekterweise müsste es Lemma W/3 heißen. Sobald ich Zeit finde werde ich die App überarbeiten.--[[Benutzer:*m.g.*|*m.g.*]] 18:17, 21. Jun. 2012 (CEST)<br /><br /> | ||
| − | + | {{pdf|Beweis_des_Basiswinkelsatzes.pdf| Hier}} finden Sie das Arbeitsblatt zum Beweis des Basiswinkelsatzes aus der Vorlesung vom 28.06.2012. | |
| − | |||
| − | |||
| − | |||
====== Beweis des Basiswinkelsatzes ====== | ====== Beweis des Basiswinkelsatzes ====== | ||
<ggb_applet width="1272" height="830" version="3.2" ggbBase64="UEsDBBQACAAIAAqm6DwAAAAAAAAAAAAAAAAxAAAAYjVhMWU3NzNjYjczMGM3NzA5YmE1ZWE2ZGM4ZDVmOTZcQmV3ZWlzc2NoZW1hLnBuZ81XaVgTWRathNUoSwNKIzTYalTSYFpFwSUsLo0Ji+mQEhFBVtkJKpsBkrjS4JIeJNCiAqKBWCEQFTACQpBWGhhhCCgoWxQVkC3soIFMJei009/XPfPNr/lTt+67VfdV3XPPee8lEZ3tNVDLUQAAaOD37iYBgJImfP9KHQlfh19G/QMANFfid9uRY18OdXr75JQvV/FqHYxuWzTgtTT80Vc30mxPbctIFY5LMxq7mnbiRnBnWrZ6IIC9VltVAADSARiQMpCNQQAcwp+5wqtgvzLAN3DPJ2zPT1wbEsTvHrBBqCFcWY4kW6GdEERf1tOOsAU34hEINfIn51iOwlm7XDtCrIWkBTXmuTRfpM8cDce2hrT6/QLnXiG2DUOMODQRmaq7wt4vToX8UpBITXutGZ6pefCP3WnHItFgEq42FtywY/IN6t1IJVr5Gk8DhVKRTm26cKmnvceAxp/lihKSQqmrNsy93TnicXmC27PmFSWXWLBoJvYqRIBS+JRVg1kmyeTnRpK2DJEVrzHsLBg0Nez4jXtVDA+fUXZdKi3qHlnqvqUSO9+0NaQsgLlC/MjYk9txeIaeHuMh5BCWktlr/ft50ITfwMfmJVduPcjrHWHG7fPvDwGDTlgmfPgtj0JRjqd7y6LB5Zl8RzClbweiu11DUDtNvyyYj6WD/ad5I2uCTvbPbloWHdk5dR0q2oG9swmUWG4nozW/njoF4nOOq8RntZcmomaauQE1OsZjPR6bh7WTjGbW9v622nwDLjGrs9zNsZB7rnIjfXVb+Zb5yRpfpqub9T6o4UycGa0ylRo/xa7Vp2XFzc7ll1PyukXx1TUPhpYxD6GYAJhE8s6aO/vGdc23B0N/Sg4zvBbvnhS63rM46NEZWi86pQbd5IasqNdaHJufdnEkd4Ur01JEKW1wasbe7Ky4W/6zLPTt09VPrXE3LwroklHfq2YcrGtL3uFDlzJaxn9V7Yjc6aRf5sJMlC31NNO6U/7QPG8a8aQQ3XW/qVNcP/DixSp//TQQjTqXMBWttd6hIelVZeyzmbf2zdalNRt9p2UvzNq831nTklqObr6+m24j/jinXldb5j/7w8V8DK/z/YHOxqgNeJkXdb0ZTfueycF/MHP01bwf/tLQ+Wb87zIfWXmVYcgY9U5N72F11T5pmMHsmsutzykgu7GrS30mrdq6sXrsaWX8oxN+mfaUE5NHk+Ptx2XNszNoncNpfR+U5teCQQ+KUgWIPAxIvWHgluOZn4dNL++NqcllBUSfzaBmvignDFk64SpK68f6fSjSBC7mNuERDaVPb96QfK6v2PieQNfEo4awY6LfId84fTeXIHNnHXFwoOxHW4q3WOMKz7OrH/t3RrGJE0q3wnIt+x45Efp73ZYIav0jgm1Edduausno+klIRKu2picjQdO0gUJXdnFPSiDYL+OS+EUTR8C7vLiPzePLw8M9Kd9WNV8Y7xldr/6u9nJvEn12eqWlVCQdnXQ6+RhKccqGRJnV1mVmhLmxX6chkt9IzzRX9OEovgiasANRBUPdXIK1WfbdfgPZDVWTcqtLmQ7tjltcuuj2oXMxHbmN9wSI1oaCMVqJn70JU9ZwvLUglFPnwpIG34GKevnYmNeex/ez29Zu8OcQKN/If3WEzK5lzQ2AtfbE/RtwvZX9AqldY2HRO/qqipuBkyfS4lg5Vx+7Gh/uuuzgITsCEaz5zuDLqDYX2T7JD+BBM92Hd12DRh1auY2SYYd8I3nGbg7htqw+ia5TY3lQgM9IoFof2enTTnytH5Dp+QKXkNlXMty/LX7Q2f3NOMJHVgGWY3j0J1WbixOCQ4+E6dOVEd1BbbruFdXYxp0WMqeWbubSvfEde1devReV27+YLtXZd2kx2P84llcRszKLq+cRTGKVWFp2f7C0aDbBWVr76pZvT2k39m3UdZtzfnhdRLknqdWtjGmNHJc57/D2sZvvpRTiTjFGNg3eDiil+7mNmZ5uTLoWdsWz3ke6K6DmsCE+zENamL7XON2RS3C2WCEudynNKOb615xVCBtNnJk6wyuso+BGJgXKh0CkIymZMNzLlW555sl0gDVUuPotM/jxfMn44EJc2Ug7AqxdrSKXU7lVNoJHFRL7SXgRC6OcB7Bah54B0frXGQwlkIfZ2gRbKAVSVrdaIYZS8Kg1pv9u1a3UBQtii+xSk4oy9+XlGsokPR2eBa0Ftd8jyGhb4cmXyK70nBvGGudetuivW5jokrHE3eVgS06F+ds+gkK+QUQlK6f2FImYtjGSfZHMHo32TTu76bIeGe21D8HkmXokYq+1f7Of3Z9rBi6SLwqEZbkSYVboUWbBwwTflHdUDy8lEC+8Mc8wGVM9RO2lnjMfxn5DruJN2lZBq8X8RIbJUfeYYOJbK/1CI3JtFoIowCyyIptIlGgHbKXa4/l8nA3n7ndxtk3w08QYIfPDV6mjUFEpZWCsKYn2MWV8vFVly48sZaNoI4kRFsJcuZUNv88hRMn5CcDLE5sb1mlbhceIszFDeZhZPqCoqj0R6b/mNuM0VJQFFXF1NQZjU5AQyXmaJUkaTFhAREJdKGQ2nFNRbV0NufNF6bNhqYAdZAH8hBdc6y8tg3GawSXI4RAe4eoAwh8OgMeaFqlbEZ99TvTfvLtCnCDEDs1GBpeOatk0DL2lDmUs0bWVNw7HXJxguvx9kxfHKeEkSdEsr/oQlZvZe8zft5MuFdzCIJCa5KUSd9MMs3Uq/qa7XF/aghldwReMH8h/SqIeG+oEM+1Vx3ABpnNk87m7HYEWeDsQSWa/h0ix7qN3yi2sJ/zOf6QX2uK2cw4VLg6V17UFxqWTUVYUpm/gU5Vfx388xz6NERQbrzsAIzClLVlFGajQ4teefPdHNHtoB4S+QdLRLIP9bZkm5BcsXHYgqBPB2S6umVevm88OiOkWfSxZb3K97z52qw3dw0sXbhrvGkTjaI77h8xwJTMjsrwdGVCkfvs6saqR/LZo483QAVVlIysqSPDoubjqaaIKgNQ0KsHsoZJaO9amMbOV4WA0iDoC3qa3/1oZB8hLCi/2u/fVVaDCU07BhYhVWWh8IutaoKIxklR/d/CfGCrva8UOSF7lBftnWyOIB++pDL3B2j1r5eRZUAkGpEBDwUj5pF9aOUM/Yz6NqCzqbb7d/8RGanU/faA4ZKMjIJ88u4QxzQ7k2J++sWVShaCYKPGmmvR56rJiDsVha6miGYmgkMIOvJutl8pe4hGkBAZRuRvq667gUZAO/yaj5nlqQbV+w9AwJCr6umtk+7JAhzWmHAIDIu8BS4uc+Iypthbjedf483GRQ0OGly1aB5CGHAJSc1JNGmEpTgGDzH463P16XmS3tOOgll4+HIlTn/G+HzXdHBL989aGx9+pgWMBgF4BHHimJv3JZJm2G7Gu+NGUNLuuYBCxh5vC2NWJsHltT1RNXO4IPUtwT2c6T7SnX8uqXM9PkutAD6M3tmkofl81VqhSH7SA9cT3+dg5ze8+8VhyDCtYFOBuKY/okdliaqMCbw7hzsA2EzuYWhFvIAtnyN4yOb5AFO5swe/BoziEE2WkJrpZ6wKjCZ8Z/YnE/yujS/5PGE0GqR0JFvK+0/mXFuNc2Udj0hZ+Bp0sKsLgXrw29oj7+GT108lSoSoEIzGHsHmjIfhoF3Onc8CgRFAZSVS5/1xJBQap2hhJE4R1+m6/oME16n3NOo2Z3QSgXNGIxPdKtHx4A2l201xrUyOqffw0puyumh4PxjsKbhETu60GzvV/Kssf7ne7RCzNwyAgHflHpRhG2P5NocjPSKxTcRdu1Bjd4xnCh4hs0NTzevwBQAH+TnDsq1Q5MqLiiajr9Gngd/bZCqfJX66Pf83e7+ECycn62f5OWm0JD0QDjItt8FoMWE2Q0lyA/3BOysY8zA7xMcHRwrENWCBiEIoMajxPbdns1NuCBBILCd4/klgAAAb50Aac4JxkNLgIILIyj8PnOSJr/5kBeFGFc6AH4G6D09bWwaAC0IKjiNz+i5nh2Jfjf/hIvWmtCN6eCn/Nmhn40Ajg9zjvLtjpdeqfUEsHCL1cAqreCwAAWw4AAFBLAwQUAAgACAAKpug8AAAAAAAAAAAAAAAAMQAAADQ2MTVhNjAxNmMzMTY4YjNiNjA3OWVjMzU5NTAyNTRkXEJld2Vpc3NjaGVtYS5wbmeNVnlcU1cafcGNRarWBRUFuiCiwkMGhKJsFQSMbOKCYnigZbGVgBgIiw+QRSpMtT9QArIEsEAoSlARNIEERHQ0LCOLyBIIINUkEGRJgCcJk5eAZRxnOv/kd8+95373fuc793u54uJkp6q8WRkAAFUHe5vDAKDAk46fKipIf1UmDW8AgLKZg431kbCuEbbH6d/t1y1zedZASFca9Frn9PXI2mI1nuqv+RF3qPjql+ll1zIVnnNXABwXp6ilQAyiAOQyAIACfjp0sYa/wwBHBluRFi+3vSd+jA0l1i/dInHGHIcAzIo2tVbV1UFW8G62FHxmqk3NCsb8OTPdEv5On9kb1TOcR+8/1VwZH+PWnZubhxiKqDvFvr5zs4LsCp3WgPY1Lu9NUr1Lio0CCnnJyNfDIfHiKdB2RzuJWpE+u/xCOPF1INaQXYFf2dwnmhoVGtOPpod4toRvfEqs1OI81hBY9uRMQyTrkSMUsHvdRmFB8RURElJ5xOtYCdhBdpyeOBhoXZMA05HgaKsMN8ii9z2obI6Dzwbkm9ud3L/kdDaSIjnV9cGhGHwc9bMRKwsZD4c3NTUbp/vTlfisSYsx00GvoV8aCN1n8tnRxDG6eFYREWMHPGJT8zQgC/YecyxiWpC0RuN+NPsozZz2U+gz/t3WUT9venY0dkxpKdtgW2VWwGGFXv/Xt8DtvX9TcQ2OdRQYlXdWHv2H7/htWHMbIbtoO1N/MwWk9gWV3XEWDj2oJ8J9ODy9577IxoS9h+zfmRZRfR7BNW2Ia23nzGSfrdUzd8K/a4gcE0re4gq66+ZUiDtG44T3TjR1lGlOra/oHt7E5EaRza0xc8x4866eOFxCqcFsql/j6JeTdYSVexzbRsi2tTniZOOc/Enat/Q8JKU7zLAE7B5JvIlXP1RuM85P/mL18mxtTyMl30axZoOf99j5AbDKAl/m3ZgDEiMv2hm0DTQaTjhumLJuVxPavg6c29G0v3zMb/+6FW/gyXzqQ9ga2VofaMaMShpnlx+GWrTTH9d+0zqSu/eHjKH2H/RMcaW/XBtu+Mm+XOd4RJb/5etNurvYGvpPZn8jbkhLJVV4CG3hNSK3h/Ynr7rusSGHJL/ZHhxaXRTUGkgeEIflZiBf6tVSwADHcsIVvU7xzImwVGbFjTyy5ill5whdSydDgi89uWDCY8MrtzY1YUJInYblky+E2iR+O5+V2WHrJtR2j3WFbmb6W/Yr3WY1aoWl23lkVMSGR4ZPmc7Qob1x/bixEdZaO9gViocTyuzoOwrWvukoATMucF9RwUBPtTvtJC9Nd/hsRP5QdHFtfZfGIGff5P21f+DJjSck517Onk+Js9tfbjK5b2RPZKRkgjxYFhR7FclnKH6o9F7llPd8+PC5u0hKZE4InzXAz69GDLuXHIM2Z/qP6TS0QISLD8jTO8f9KLssnCIEWFE8J6G7ddChQKwrU2W0zjNCZzqf8S1Ll5z1IeXi65CxNQw4iUhN3sbHcgO0ogtijH2ruBUzNpmi75WL8taJnHsFmGo4a7iYPmH8psc1v8Gv4EJ0szYEpVmOit3Mtr59mXZ5d7QK6lGVIuFlot1XSZaYaeTnkP4WlYRzB/i7J3QkQreqcNyWcoaNR7BgKuORABvqcAAuDkyDhcSe3lOvzpoFTUZcHtB8bqaHe6FP0Q2UcB8bP1AmE3nPpudUVrm7H4qKErboKYZleoPmLSMpB+sTV5bqmYxudpi0eOQyNHgLU+DWL+HqJlGxhdeYyGkaRqFUUYiNLPNU4yVzlxeq36h+piYx5dauyqxAaPIm8+Jt4tbZ1dgSKlbWf/xEx/p6uV/dYegL6wlLlm5xgQ6ZWNVYS2v4+d7V9TsIADfKEAV3GLMZt9DCFtGkamMWwmDkMaVuWrao36Hk1e+ZpeDbPLqn0kNNRynzEo/PuvUoS9oMay7FtZHCr3w8H+2PUiBc5gKhq7KQraoygPbNhcg1hLVB/zGJXsen2dpAVFTzx9anhCVokEX3QoGLNPSixGUrn6EZsOdppvYwBqDEt6vV8FT++Q5VWdE0l5GOj4lZIgcUkKeixYmRFeMLCliorsXJZVDAj+tyclzMnA/83So2QZeDN81Edx/tIN11lty0tryJogevSPzHrJI7h1gG6mob5SrMTIkM/36W3Dm7OoW7nKeSy7j9LtTgOXpajTePFSD04afOJ+TTLronTrw2D/TOMFk6RY5ysL6/6Fc0t0sv+KyCquFW3DwpW3CPNRQ6T7olMBRllj5Jx0u/cjwWlcbSPdM9aF+oLk0DuYcnnu80kwY4yf+YjxdN6f/NW/qcgYX1ebICwx0CgB3ewmVSWxnRFkeYZ0i/cAp/LbMWJ/oE1LTfBKc87ymaNEU6oW5G0neG6Ry3m416gwRdJ0k6cTk+vomS07RLiAIF3PlqE2oYjr1wKGLSP/H+goiqH3ZVzUvwY6PPs2aNDDkwE2juM8umcc55ok7O7ULGJ04ldtKY89wkPNZAXdPKUH7cDX5yO2rqwTYS/+U3HejboFQw9lkEGwnXy1EVI14zo5d/D5Tr+0n2shsukoLyX2jc5XJQ48pTAay0bzOAY1DMgeOf+vjzT/szb3Zp1VUkWIPWWiyX8kwbySNctvHqYUhjSMY3PQA/uk7CbwxUPSBLhMnoecGauQvcQivc5imlDdnJeDbwI0Kan7dsO48K3h+XeaANgmLloyMQVNh8sEigUycrcEg76WL23YWKo5omoyLEyK2zhfqnDQrV/80Tciti/upRnsOhdhtzRR8y0fzpNQCQlhtoUwOkTeZ/DCVPox0r9X9rWtkXI/0zCTjYOtmUfu8V+y9QSwcIIGKtYUkIAABzCgAAUEsDBBQACAAIAAqm6DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7V3bcuO2Gb5unoKjzuRqzcUZZGOnIzvbaWY23Uy8XXc6O7NDUZCMmCK1JOVTJ2/TF0hzm7vc7zMVAA8SJVIiRdsrt/GNRBCEgO/7T/gB0Md/vp0F1rWIExmFJwNog4ElQj8ay3B6MlikkyNn8OevvzieimgqRrFnTaJ45qUnA2yjgS5fyK+/+MNxchndWF5gqryT4uZkMPGCRAysZB4Lb5xcCpFWyr3FrQykF9+9Gf0o/DRZ3sga+TacL9SvpPFClfmz8WuZFJcvzQ/OA5l+I6/lWMRWEPknA0ZV19W3dyJOpe8FJwMCshJ0MkBrN1UR1ncvo1jeR2Gqqy8bn6gSy0rkvVBPAl12/NIM9Fgs/ECOpRfqwZh+qEqWdSPH6aVCD3Gk2hRyeqk66yAna86Ponh8fpekYmbd/lPEkarpYpszl7oMui5FxOED6y67dYSI7XKAgcMdh7oOo46CUfVZdYa4tksAg5xyDl0OCVWPNd8zvy6uz0WaKjoTy7sVS6CnsRxXLr5NTqNgWTSPZJieefN0ERtZwHnReXqnf06BF+txDsNpIPIyNXj/UvhXo+j23IAHcdb027u5ecR0aDQ9i4IotmJNixrANP8cZZ+mju5pWQuYOsDUyNvQjZb3oYtMDfM5yj5NrUCGWdfykcNi1BAUPyMTSxeoxrUIl4MPvJFQIjGwFqFMXxcXSnSu8qHC7IG/LWYjpTurwlO2CR+qzeOXa2J3fCXiUASZbIWK20W0SKxrLcTZb5mOjIUvZ+oyu5FD4mm6/q46kJWOxTQWRcczzcsAM3fBqvyuFR+/LDqh+5CovvqpMiFqPKkey6m4EQqHsUisUy+RyY0Mr0SQeOm9SLT2p0rzTgYze2oPrLGXqie0NRGBmAmle6mRl3AxE7H0S+TOlXDpVoLf/h1OxUB3TfVnkfeK2Xl3jS2KjFkpDEjewJIkdbtBvJQBml966psNcyHy7pSJWcXDtPZdNM5/OK+XBMYWzaQyo1Sb0Zl3qyVNf/VGSRQsUnHuK7TD15HvpcbcZr3LrYcySLqueogQ/eVOjQkZgzyRt2KpmKs2a4XupbCnl0qmQpEkRiPTVd3zQiUShidljea5vU/mQjdvvhe1rbkat9H78ieUGGb0bBBl7EKJ8nDQlwVjDkoewFYe3kwmiUg1akcYG9AQqqUpf8hgmZUsO2IkPNGNgBz5I66/3GeomDqZ8dPm3jyMu0By+pkgcTNAWA9AnL0B8aPZzAvHVujNFCDnYqrLDRBSO3fLA1pWLA9qfLLBL9Lihp+1lrexAW+St1YA6A9aq8BDmYf2YkkyFraRsCmATg43Le1aq9GJj2FWJ8l8ipypQMmXaQlwoLX62zBVHkYYi73pOK6EmGuP/SZ8G3thoiO+qnw0s3wmYz8Q9SSvme91xsfbGVdOZsUVjPfku+qKH5LwDUrb0SWnIrxWXYvixLJuQW6F70AuCPdFya0C8CiTDZgX3cMVZVRWPZa31rCoPyxqDZEOw8w3nDc6JEVbQ3oy4HaD6Ci34MuJ9Pdg/LQV46IL4+J3xjswzvkm484DMV4ajzXSxxnpeg6HVvq5QvjZdsKrPvNsL5/JiOFSf4yyj+4GG+YeD5J2JruI1o6QTRF3GAGEAgAIAuTRPObZBrijbh5zdAgeE9YTgAo8t6rbkoAjYhOOIKYuJa6aTzvmcZJ7UOQ8Jw9az/ppE+teN9a9w2U9D3v6MH5UUM5tzjlwOMPqJmOYPx/+h+F0EXjxqUyMj2jSfmNjN8PmyXZx0ACUNE4O36MuCYe5jQU5w4bqhyG1u6ebZCz4G/BfdHFwF60dnIqExjKbtavab/LKVw/o/bYgj1Hh3sxURIPv7OfQfvDu1oA8y4C82ADyZjuQsWqpgOnmYU1aa6z7zgvzWWHrGKPG3pXKALntOA4l2IHqroM38p+Ha+86+rtpN383bRYOnZtuKR0rI60XD7kpHuupbQofQhkf0O9tjP8gBaEx3L3sJgiX/xeC0DLk/fzUV8mSM2+6BPlUBmNo6JpI1aVMOkbUg4Jz7I84Br4ScnfkUeGxse+M6cRl77MFh8S/FDPPnofTrFMyPPX8q2kcLcLxRo+T1IvT77ULs0Kz5mIMuTG2XCvQ8q+Y3gFUndD1DZ5WOrPbtcAdoXSbzG4XDtA6B4RB6jEAmY8hc0Z4xAB3ha9lECBKxq05WFnGbaaAVCjIDZ3OZPXmoEmlPwMFt/NY9Vdbkbw7b8VtqgyEunEy+PLjIkq/2raSltUwrVbZTFUzg2qbDwjDrkndJgx6QT0RsZwsNwaYBWI2KEwO2BCILBtOHbD6B3M5sHFFDHaDiiqgvotib5GoSOx+EU7bo4jao1jvH358NIjXgIPELnUG2MRpBKsy4FEUBcILy/H8uL7Iumo9n0aWlgGzg3jm5LjbDMRuQcAVQfCs94qpqTVqLwS4rxDUBAkPJAQyee29Ff/YYmWzJT3MStEAZE299pETeUhyQklmJIizZcltt5yQipz8VQbBJLnKdjpcGUrvF7GVGefJb79exp0MCTlMcwxKc4xqJcctJYfYmHQzwLSC54XxYpdeMJIiFqHq4I11rR5oDyHtq4a95vRdbLFrK0nMUXO7gcYqoL03u3es4dlpe5jY4cLUzlopT4ZL+Eiz0G01UFeHZKBYPltDgPYxUHwtTJzGv/0ajpUZsvQ+JGWwqvaqvcjw52ucakJFatNuOudUcH11K5NUhPeWnr28kspSLVI5vRIyNTBv2LEOODt9VTN4OgvmVqLwXB+ZDZuj8K36GByWPhb7pHoFDO5DzDDc56p7iBVJEtg82aif7oK+EblqoacmzT63k1Pt0tqUE4LuWh5kH32bHZa+ZWsfbi91g+tpkktvMU87KRs80KzILm2DyGasxh4r3asKEW+Slo01540tXGfFzkyz0jzMQVjm3z/9J2uzKQFvQtUSSFV7TQCB7RAImMM4oIy7GKBd0rhrjS5sIgqCTarabu7ukmT0Yn+5Fqp/NCsNgujmBzEJxK3BucNGgKZ9dcOMlM1FkU8/dyLl599J2UlKg/FBaxMzPYTccb0fidTrYIR6JxUbMX4q54VtVlqgPQPC8JAclINo5qC2gNNCRqqZxr9EwVToLJGl4sK+UzTYIQl5SJ5rmUBitjIwjgOBi11MuQs7ztJgNT/3KlFXaqamZmGpdfHC4HvuX4YyVcYxvEpNcunGmqlpWweUO6Tp6lUzesIZGmeEqqmMixxGGSsObWC0xBhw3BHkatLufXQtYm11/zU8/akDjL1TdY8HY0sLx21CKEbMdSHjRf5GybBDOMUOI4Rw4LA9g/PokGxfMTi87RhVC8lhW7NTpTHsIEUdMpkHZvIo5dDFDmSOQwrNdGwAHBdylxIHUtYcqjfgW83+vRYq4LNgBzQ7JPnqdXL+VKbNzI0ZpZAjArGKSgsAGXAZhtiFCACX7rl0NT8o5cvjKOzwdsq3e8pQ3TG8udPy0y8fhp0mDbr+xrSBI5cjZRgZUjaSMdx32vBxE1sI8lPeANWciHz0qYP7CNO5ix27uRXWpx25Of2dmx6zumrq//3UU6h/GBbzuuyyw9ob7J3hr8H6ibcKQJdgAgCHmGBGym0DDCOAMXKx8lyus6ft/XhItrfYNkC3HftqIUPVZYAbS01KNleJzHTk0y8dRKnDwkC9KMVP5q+x8syAK+9czO9yqYE20m9IQS5xHA6w2zzj2yo18SFJjX7JSyY1Ww7Zd9303HgsItnuDdY3PSdPs+k53YQVUrwCrLnaV7oe4wzEAWyArt+kCBrm22cXPxVeaLWsw87F3ktkNSw/qSvitusSFWAg6iJIEYKsNCsEIpeVFmfPDGR6SGaFkmwiQEnLiUCDPFXXyNJYXksv6CA1HRbI6qVm8WReh9qclREJd5bS4biYYkghgICDPYVjcUjCUfoc0nIjbNXnfB8Fd9MorJ8nXjQtLb2Tqj3/CuZHHz/ArKJnvuCTwc0HuN05zfOfLcApG2wd8/cQw+tNFspzOSA7LWk+Sy7oBhdt02Hb31Pz4aHH235Ie/vd4pU0z+VA/Y4j8HtT0OrsziNxUH/eqwh+ntX5z+303DxHDdl+KvPo0BWm6h++k3Hc9OKBmw2/MPzSm0fJV7tsf+UFcfkjvZ3nrpei4Xbsla84Y7Zb/evz+pZaGC+aYLzoDuNFE4xtXtDQ6U0BLXHUbwqo24Db87UBtUCeNQF51h3Isz7y+BhAPtILhRoCv3z0WfhXXqAKlLWh4OqD/uqDXnmhA8N2hNQHhyvMPIMQcQu9HULERxlzHyfY2oyqyTd3CHS50n1E0aujYo6Oaw3rEeJr5UUO7SC95I6wshdtjxJatuSt4Z0SDXT+j0Wbz1XZ1jjjbmWGdrT+IhB80BTV565Q096ji7PNZOipKuyQ1+q957LGW7RP62zluG02VG88yneUQAiLs94qBHMxZy5GCGGtovvlu64/T75rFZiaZGi/A72ouh8TvrDQCwu/sM4vzjtITu/T3/ePJjmbGVHoIGUBOCQMUUJ4KSOUry7q7pkTvT8kGSlzonzLGwRbyEh1V+lwkVjEmkTBNLUW4UymqQhGXmyNpbCWB07sL/8IweoWtz91kKdHPwneRWSIzV2gt4swChmgqFjvx7ZDqcMQYI7LKEXN6/31qFa3kX4jJjLMFEPvBfwmFlLF+non9FSNPLzvgF7vnaWjD/CpwKU2oRA4KgCg0CEYFCsUSk2VPgIVanEHALTnCedRnjc7EH0kKItIOGxps1+u/hcJfV38x5mv/wtQSwcI8ERz8voNAACjZgAAUEsBAhQAFAAIAAgACqboPL1cAqreCwAAWw4AADEAAAAAAAAAAAAAAAAAAAAAAGI1YTFlNzczY2I3MzBjNzcwOWJhNWVhNmRjOGQ1Zjk2XEJld2Vpc3NjaGVtYS5wbmdQSwECFAAUAAgACAAKpug8IGKtYUkIAABzCgAAMQAAAAAAAAAAAAAAAAA9DAAANDYxNWE2MDE2YzMxNjhiM2I2MDc5ZWMzNTk1MDI1NGRcQmV3ZWlzc2NoZW1hLnBuZ1BLAQIUABQACAAIAAqm6DzwRHPy+g0AAKNmAAAMAAAAAAAAAAAAAAAAAOUUAABnZW9nZWJyYS54bWxQSwUGAAAAAAMAAwD4AAAAGSMAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" /> | <ggb_applet width="1272" height="830" version="3.2" ggbBase64="UEsDBBQACAAIAAqm6DwAAAAAAAAAAAAAAAAxAAAAYjVhMWU3NzNjYjczMGM3NzA5YmE1ZWE2ZGM4ZDVmOTZcQmV3ZWlzc2NoZW1hLnBuZ81XaVgTWRathNUoSwNKIzTYalTSYFpFwSUsLo0Ji+mQEhFBVtkJKpsBkrjS4JIeJNCiAqKBWCEQFTACQpBWGhhhCCgoWxQVkC3soIFMJei009/XPfPNr/lTt+67VfdV3XPPee8lEZ3tNVDLUQAAaOD37iYBgJImfP9KHQlfh19G/QMANFfid9uRY18OdXr75JQvV/FqHYxuWzTgtTT80Vc30mxPbctIFY5LMxq7mnbiRnBnWrZ6IIC9VltVAADSARiQMpCNQQAcwp+5wqtgvzLAN3DPJ2zPT1wbEsTvHrBBqCFcWY4kW6GdEERf1tOOsAU34hEINfIn51iOwlm7XDtCrIWkBTXmuTRfpM8cDce2hrT6/QLnXiG2DUOMODQRmaq7wt4vToX8UpBITXutGZ6pefCP3WnHItFgEq42FtywY/IN6t1IJVr5Gk8DhVKRTm26cKmnvceAxp/lihKSQqmrNsy93TnicXmC27PmFSWXWLBoJvYqRIBS+JRVg1kmyeTnRpK2DJEVrzHsLBg0Nez4jXtVDA+fUXZdKi3qHlnqvqUSO9+0NaQsgLlC/MjYk9txeIaeHuMh5BCWktlr/ft50ITfwMfmJVduPcjrHWHG7fPvDwGDTlgmfPgtj0JRjqd7y6LB5Zl8RzClbweiu11DUDtNvyyYj6WD/ad5I2uCTvbPbloWHdk5dR0q2oG9swmUWG4nozW/njoF4nOOq8RntZcmomaauQE1OsZjPR6bh7WTjGbW9v622nwDLjGrs9zNsZB7rnIjfXVb+Zb5yRpfpqub9T6o4UycGa0ylRo/xa7Vp2XFzc7ll1PyukXx1TUPhpYxD6GYAJhE8s6aO/vGdc23B0N/Sg4zvBbvnhS63rM46NEZWi86pQbd5IasqNdaHJufdnEkd4Ur01JEKW1wasbe7Ky4W/6zLPTt09VPrXE3LwroklHfq2YcrGtL3uFDlzJaxn9V7Yjc6aRf5sJMlC31NNO6U/7QPG8a8aQQ3XW/qVNcP/DixSp//TQQjTqXMBWttd6hIelVZeyzmbf2zdalNRt9p2UvzNq831nTklqObr6+m24j/jinXldb5j/7w8V8DK/z/YHOxqgNeJkXdb0ZTfueycF/MHP01bwf/tLQ+Wb87zIfWXmVYcgY9U5N72F11T5pmMHsmsutzykgu7GrS30mrdq6sXrsaWX8oxN+mfaUE5NHk+Ptx2XNszNoncNpfR+U5teCQQ+KUgWIPAxIvWHgluOZn4dNL++NqcllBUSfzaBmvignDFk64SpK68f6fSjSBC7mNuERDaVPb96QfK6v2PieQNfEo4awY6LfId84fTeXIHNnHXFwoOxHW4q3WOMKz7OrH/t3RrGJE0q3wnIt+x45Efp73ZYIav0jgm1Edduausno+klIRKu2picjQdO0gUJXdnFPSiDYL+OS+EUTR8C7vLiPzePLw8M9Kd9WNV8Y7xldr/6u9nJvEn12eqWlVCQdnXQ6+RhKccqGRJnV1mVmhLmxX6chkt9IzzRX9OEovgiasANRBUPdXIK1WfbdfgPZDVWTcqtLmQ7tjltcuuj2oXMxHbmN9wSI1oaCMVqJn70JU9ZwvLUglFPnwpIG34GKevnYmNeex/ez29Zu8OcQKN/If3WEzK5lzQ2AtfbE/RtwvZX9AqldY2HRO/qqipuBkyfS4lg5Vx+7Gh/uuuzgITsCEaz5zuDLqDYX2T7JD+BBM92Hd12DRh1auY2SYYd8I3nGbg7htqw+ia5TY3lQgM9IoFof2enTTnytH5Dp+QKXkNlXMty/LX7Q2f3NOMJHVgGWY3j0J1WbixOCQ4+E6dOVEd1BbbruFdXYxp0WMqeWbubSvfEde1devReV27+YLtXZd2kx2P84llcRszKLq+cRTGKVWFp2f7C0aDbBWVr76pZvT2k39m3UdZtzfnhdRLknqdWtjGmNHJc57/D2sZvvpRTiTjFGNg3eDiil+7mNmZ5uTLoWdsWz3ke6K6DmsCE+zENamL7XON2RS3C2WCEudynNKOb615xVCBtNnJk6wyuso+BGJgXKh0CkIymZMNzLlW555sl0gDVUuPotM/jxfMn44EJc2Ug7AqxdrSKXU7lVNoJHFRL7SXgRC6OcB7Bah54B0frXGQwlkIfZ2gRbKAVSVrdaIYZS8Kg1pv9u1a3UBQtii+xSk4oy9+XlGsokPR2eBa0Ftd8jyGhb4cmXyK70nBvGGudetuivW5jokrHE3eVgS06F+ds+gkK+QUQlK6f2FImYtjGSfZHMHo32TTu76bIeGe21D8HkmXokYq+1f7Of3Z9rBi6SLwqEZbkSYVboUWbBwwTflHdUDy8lEC+8Mc8wGVM9RO2lnjMfxn5DruJN2lZBq8X8RIbJUfeYYOJbK/1CI3JtFoIowCyyIptIlGgHbKXa4/l8nA3n7ndxtk3w08QYIfPDV6mjUFEpZWCsKYn2MWV8vFVly48sZaNoI4kRFsJcuZUNv88hRMn5CcDLE5sb1mlbhceIszFDeZhZPqCoqj0R6b/mNuM0VJQFFXF1NQZjU5AQyXmaJUkaTFhAREJdKGQ2nFNRbV0NufNF6bNhqYAdZAH8hBdc6y8tg3GawSXI4RAe4eoAwh8OgMeaFqlbEZ99TvTfvLtCnCDEDs1GBpeOatk0DL2lDmUs0bWVNw7HXJxguvx9kxfHKeEkSdEsr/oQlZvZe8zft5MuFdzCIJCa5KUSd9MMs3Uq/qa7XF/aghldwReMH8h/SqIeG+oEM+1Vx3ABpnNk87m7HYEWeDsQSWa/h0ix7qN3yi2sJ/zOf6QX2uK2cw4VLg6V17UFxqWTUVYUpm/gU5Vfx388xz6NERQbrzsAIzClLVlFGajQ4teefPdHNHtoB4S+QdLRLIP9bZkm5BcsXHYgqBPB2S6umVevm88OiOkWfSxZb3K97z52qw3dw0sXbhrvGkTjaI77h8xwJTMjsrwdGVCkfvs6saqR/LZo483QAVVlIysqSPDoubjqaaIKgNQ0KsHsoZJaO9amMbOV4WA0iDoC3qa3/1oZB8hLCi/2u/fVVaDCU07BhYhVWWh8IutaoKIxklR/d/CfGCrva8UOSF7lBftnWyOIB++pDL3B2j1r5eRZUAkGpEBDwUj5pF9aOUM/Yz6NqCzqbb7d/8RGanU/faA4ZKMjIJ88u4QxzQ7k2J++sWVShaCYKPGmmvR56rJiDsVha6miGYmgkMIOvJutl8pe4hGkBAZRuRvq667gUZAO/yaj5nlqQbV+w9AwJCr6umtk+7JAhzWmHAIDIu8BS4uc+Iypthbjedf483GRQ0OGly1aB5CGHAJSc1JNGmEpTgGDzH463P16XmS3tOOgll4+HIlTn/G+HzXdHBL989aGx9+pgWMBgF4BHHimJv3JZJm2G7Gu+NGUNLuuYBCxh5vC2NWJsHltT1RNXO4IPUtwT2c6T7SnX8uqXM9PkutAD6M3tmkofl81VqhSH7SA9cT3+dg5ze8+8VhyDCtYFOBuKY/okdliaqMCbw7hzsA2EzuYWhFvIAtnyN4yOb5AFO5swe/BoziEE2WkJrpZ6wKjCZ8Z/YnE/yujS/5PGE0GqR0JFvK+0/mXFuNc2Udj0hZ+Bp0sKsLgXrw29oj7+GT108lSoSoEIzGHsHmjIfhoF3Onc8CgRFAZSVS5/1xJBQap2hhJE4R1+m6/oME16n3NOo2Z3QSgXNGIxPdKtHx4A2l201xrUyOqffw0puyumh4PxjsKbhETu60GzvV/Kssf7ne7RCzNwyAgHflHpRhG2P5NocjPSKxTcRdu1Bjd4xnCh4hs0NTzevwBQAH+TnDsq1Q5MqLiiajr9Gngd/bZCqfJX66Pf83e7+ECycn62f5OWm0JD0QDjItt8FoMWE2Q0lyA/3BOysY8zA7xMcHRwrENWCBiEIoMajxPbdns1NuCBBILCd4/klgAAAb50Aac4JxkNLgIILIyj8PnOSJr/5kBeFGFc6AH4G6D09bWwaAC0IKjiNz+i5nh2Jfjf/hIvWmtCN6eCn/Nmhn40Ajg9zjvLtjpdeqfUEsHCL1cAqreCwAAWw4AAFBLAwQUAAgACAAKpug8AAAAAAAAAAAAAAAAMQAAADQ2MTVhNjAxNmMzMTY4YjNiNjA3OWVjMzU5NTAyNTRkXEJld2Vpc3NjaGVtYS5wbmeNVnlcU1cafcGNRarWBRUFuiCiwkMGhKJsFQSMbOKCYnigZbGVgBgIiw+QRSpMtT9QArIEsEAoSlARNIEERHQ0LCOLyBIIINUkEGRJgCcJk5eAZRxnOv/kd8+95373fuc793u54uJkp6q8WRkAAFUHe5vDAKDAk46fKipIf1UmDW8AgLKZg431kbCuEbbH6d/t1y1zedZASFca9Frn9PXI2mI1nuqv+RF3qPjql+ll1zIVnnNXABwXp6ilQAyiAOQyAIACfjp0sYa/wwBHBluRFi+3vSd+jA0l1i/dInHGHIcAzIo2tVbV1UFW8G62FHxmqk3NCsb8OTPdEv5On9kb1TOcR+8/1VwZH+PWnZubhxiKqDvFvr5zs4LsCp3WgPY1Lu9NUr1Lio0CCnnJyNfDIfHiKdB2RzuJWpE+u/xCOPF1INaQXYFf2dwnmhoVGtOPpod4toRvfEqs1OI81hBY9uRMQyTrkSMUsHvdRmFB8RURElJ5xOtYCdhBdpyeOBhoXZMA05HgaKsMN8ii9z2obI6Dzwbkm9ud3L/kdDaSIjnV9cGhGHwc9bMRKwsZD4c3NTUbp/vTlfisSYsx00GvoV8aCN1n8tnRxDG6eFYREWMHPGJT8zQgC/YecyxiWpC0RuN+NPsozZz2U+gz/t3WUT9venY0dkxpKdtgW2VWwGGFXv/Xt8DtvX9TcQ2OdRQYlXdWHv2H7/htWHMbIbtoO1N/MwWk9gWV3XEWDj2oJ8J9ODy9577IxoS9h+zfmRZRfR7BNW2Ia23nzGSfrdUzd8K/a4gcE0re4gq66+ZUiDtG44T3TjR1lGlOra/oHt7E5EaRza0xc8x4866eOFxCqcFsql/j6JeTdYSVexzbRsi2tTniZOOc/Enat/Q8JKU7zLAE7B5JvIlXP1RuM85P/mL18mxtTyMl30axZoOf99j5AbDKAl/m3ZgDEiMv2hm0DTQaTjhumLJuVxPavg6c29G0v3zMb/+6FW/gyXzqQ9ga2VofaMaMShpnlx+GWrTTH9d+0zqSu/eHjKH2H/RMcaW/XBtu+Mm+XOd4RJb/5etNurvYGvpPZn8jbkhLJVV4CG3hNSK3h/Ynr7rusSGHJL/ZHhxaXRTUGkgeEIflZiBf6tVSwADHcsIVvU7xzImwVGbFjTyy5ill5whdSydDgi89uWDCY8MrtzY1YUJInYblky+E2iR+O5+V2WHrJtR2j3WFbmb6W/Yr3WY1aoWl23lkVMSGR4ZPmc7Qob1x/bixEdZaO9gViocTyuzoOwrWvukoATMucF9RwUBPtTvtJC9Nd/hsRP5QdHFtfZfGIGff5P21f+DJjSck517Onk+Js9tfbjK5b2RPZKRkgjxYFhR7FclnKH6o9F7llPd8+PC5u0hKZE4InzXAz69GDLuXHIM2Z/qP6TS0QISLD8jTO8f9KLssnCIEWFE8J6G7ddChQKwrU2W0zjNCZzqf8S1Ll5z1IeXi65CxNQw4iUhN3sbHcgO0ogtijH2ruBUzNpmi75WL8taJnHsFmGo4a7iYPmH8psc1v8Gv4EJ0szYEpVmOit3Mtr59mXZ5d7QK6lGVIuFlot1XSZaYaeTnkP4WlYRzB/i7J3QkQreqcNyWcoaNR7BgKuORABvqcAAuDkyDhcSe3lOvzpoFTUZcHtB8bqaHe6FP0Q2UcB8bP1AmE3nPpudUVrm7H4qKErboKYZleoPmLSMpB+sTV5bqmYxudpi0eOQyNHgLU+DWL+HqJlGxhdeYyGkaRqFUUYiNLPNU4yVzlxeq36h+piYx5dauyqxAaPIm8+Jt4tbZ1dgSKlbWf/xEx/p6uV/dYegL6wlLlm5xgQ6ZWNVYS2v4+d7V9TsIADfKEAV3GLMZt9DCFtGkamMWwmDkMaVuWrao36Hk1e+ZpeDbPLqn0kNNRynzEo/PuvUoS9oMay7FtZHCr3w8H+2PUiBc5gKhq7KQraoygPbNhcg1hLVB/zGJXsen2dpAVFTzx9anhCVokEX3QoGLNPSixGUrn6EZsOdppvYwBqDEt6vV8FT++Q5VWdE0l5GOj4lZIgcUkKeixYmRFeMLCliorsXJZVDAj+tyclzMnA/83So2QZeDN81Edx/tIN11lty0tryJogevSPzHrJI7h1gG6mob5SrMTIkM/36W3Dm7OoW7nKeSy7j9LtTgOXpajTePFSD04afOJ+TTLronTrw2D/TOMFk6RY5ysL6/6Fc0t0sv+KyCquFW3DwpW3CPNRQ6T7olMBRllj5Jx0u/cjwWlcbSPdM9aF+oLk0DuYcnnu80kwY4yf+YjxdN6f/NW/qcgYX1ebICwx0CgB3ewmVSWxnRFkeYZ0i/cAp/LbMWJ/oE1LTfBKc87ymaNEU6oW5G0neG6Ry3m416gwRdJ0k6cTk+vomS07RLiAIF3PlqE2oYjr1wKGLSP/H+goiqH3ZVzUvwY6PPs2aNDDkwE2juM8umcc55ok7O7ULGJ04ldtKY89wkPNZAXdPKUH7cDX5yO2rqwTYS/+U3HejboFQw9lkEGwnXy1EVI14zo5d/D5Tr+0n2shsukoLyX2jc5XJQ48pTAay0bzOAY1DMgeOf+vjzT/szb3Zp1VUkWIPWWiyX8kwbySNctvHqYUhjSMY3PQA/uk7CbwxUPSBLhMnoecGauQvcQivc5imlDdnJeDbwI0Kan7dsO48K3h+XeaANgmLloyMQVNh8sEigUycrcEg76WL23YWKo5omoyLEyK2zhfqnDQrV/80Tciti/upRnsOhdhtzRR8y0fzpNQCQlhtoUwOkTeZ/DCVPox0r9X9rWtkXI/0zCTjYOtmUfu8V+y9QSwcIIGKtYUkIAABzCgAAUEsDBBQACAAIAAqm6DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7V3bcuO2Gb5unoKjzuRqzcUZZGOnIzvbaWY23Uy8XXc6O7NDUZCMmCK1JOVTJ2/TF0hzm7vc7zMVAA8SJVIiRdsrt/GNRBCEgO/7T/gB0Md/vp0F1rWIExmFJwNog4ElQj8ay3B6MlikkyNn8OevvzieimgqRrFnTaJ45qUnA2yjgS5fyK+/+MNxchndWF5gqryT4uZkMPGCRAysZB4Lb5xcCpFWyr3FrQykF9+9Gf0o/DRZ3sga+TacL9SvpPFClfmz8WuZFJcvzQ/OA5l+I6/lWMRWEPknA0ZV19W3dyJOpe8FJwMCshJ0MkBrN1UR1ncvo1jeR2Gqqy8bn6gSy0rkvVBPAl12/NIM9Fgs/ECOpRfqwZh+qEqWdSPH6aVCD3Gk2hRyeqk66yAna86Ponh8fpekYmbd/lPEkarpYpszl7oMui5FxOED6y67dYSI7XKAgcMdh7oOo46CUfVZdYa4tksAg5xyDl0OCVWPNd8zvy6uz0WaKjoTy7sVS6CnsRxXLr5NTqNgWTSPZJieefN0ERtZwHnReXqnf06BF+txDsNpIPIyNXj/UvhXo+j23IAHcdb027u5ecR0aDQ9i4IotmJNixrANP8cZZ+mju5pWQuYOsDUyNvQjZb3oYtMDfM5yj5NrUCGWdfykcNi1BAUPyMTSxeoxrUIl4MPvJFQIjGwFqFMXxcXSnSu8qHC7IG/LWYjpTurwlO2CR+qzeOXa2J3fCXiUASZbIWK20W0SKxrLcTZb5mOjIUvZ+oyu5FD4mm6/q46kJWOxTQWRcczzcsAM3fBqvyuFR+/LDqh+5CovvqpMiFqPKkey6m4EQqHsUisUy+RyY0Mr0SQeOm9SLT2p0rzTgYze2oPrLGXqie0NRGBmAmle6mRl3AxE7H0S+TOlXDpVoLf/h1OxUB3TfVnkfeK2Xl3jS2KjFkpDEjewJIkdbtBvJQBml966psNcyHy7pSJWcXDtPZdNM5/OK+XBMYWzaQyo1Sb0Zl3qyVNf/VGSRQsUnHuK7TD15HvpcbcZr3LrYcySLqueogQ/eVOjQkZgzyRt2KpmKs2a4XupbCnl0qmQpEkRiPTVd3zQiUShidljea5vU/mQjdvvhe1rbkat9H78ieUGGb0bBBl7EKJ8nDQlwVjDkoewFYe3kwmiUg1akcYG9AQqqUpf8hgmZUsO2IkPNGNgBz5I66/3GeomDqZ8dPm3jyMu0By+pkgcTNAWA9AnL0B8aPZzAvHVujNFCDnYqrLDRBSO3fLA1pWLA9qfLLBL9Lihp+1lrexAW+St1YA6A9aq8BDmYf2YkkyFraRsCmATg43Le1aq9GJj2FWJ8l8ipypQMmXaQlwoLX62zBVHkYYi73pOK6EmGuP/SZ8G3thoiO+qnw0s3wmYz8Q9SSvme91xsfbGVdOZsUVjPfku+qKH5LwDUrb0SWnIrxWXYvixLJuQW6F70AuCPdFya0C8CiTDZgX3cMVZVRWPZa31rCoPyxqDZEOw8w3nDc6JEVbQ3oy4HaD6Ci34MuJ9Pdg/LQV46IL4+J3xjswzvkm484DMV4ajzXSxxnpeg6HVvq5QvjZdsKrPvNsL5/JiOFSf4yyj+4GG+YeD5J2JruI1o6QTRF3GAGEAgAIAuTRPObZBrijbh5zdAgeE9YTgAo8t6rbkoAjYhOOIKYuJa6aTzvmcZJ7UOQ8Jw9az/ppE+teN9a9w2U9D3v6MH5UUM5tzjlwOMPqJmOYPx/+h+F0EXjxqUyMj2jSfmNjN8PmyXZx0ACUNE4O36MuCYe5jQU5w4bqhyG1u6ebZCz4G/BfdHFwF60dnIqExjKbtavab/LKVw/o/bYgj1Hh3sxURIPv7OfQfvDu1oA8y4C82ADyZjuQsWqpgOnmYU1aa6z7zgvzWWHrGKPG3pXKALntOA4l2IHqroM38p+Ha+86+rtpN383bRYOnZtuKR0rI60XD7kpHuupbQofQhkf0O9tjP8gBaEx3L3sJgiX/xeC0DLk/fzUV8mSM2+6BPlUBmNo6JpI1aVMOkbUg4Jz7I84Br4ScnfkUeGxse+M6cRl77MFh8S/FDPPnofTrFMyPPX8q2kcLcLxRo+T1IvT77ULs0Kz5mIMuTG2XCvQ8q+Y3gFUndD1DZ5WOrPbtcAdoXSbzG4XDtA6B4RB6jEAmY8hc0Z4xAB3ha9lECBKxq05WFnGbaaAVCjIDZ3OZPXmoEmlPwMFt/NY9Vdbkbw7b8VtqgyEunEy+PLjIkq/2raSltUwrVbZTFUzg2qbDwjDrkndJgx6QT0RsZwsNwaYBWI2KEwO2BCILBtOHbD6B3M5sHFFDHaDiiqgvotib5GoSOx+EU7bo4jao1jvH358NIjXgIPELnUG2MRpBKsy4FEUBcILy/H8uL7Iumo9n0aWlgGzg3jm5LjbDMRuQcAVQfCs94qpqTVqLwS4rxDUBAkPJAQyee29Ff/YYmWzJT3MStEAZE299pETeUhyQklmJIizZcltt5yQipz8VQbBJLnKdjpcGUrvF7GVGefJb79exp0MCTlMcwxKc4xqJcctJYfYmHQzwLSC54XxYpdeMJIiFqHq4I11rR5oDyHtq4a95vRdbLFrK0nMUXO7gcYqoL03u3es4dlpe5jY4cLUzlopT4ZL+Eiz0G01UFeHZKBYPltDgPYxUHwtTJzGv/0ajpUZsvQ+JGWwqvaqvcjw52ucakJFatNuOudUcH11K5NUhPeWnr28kspSLVI5vRIyNTBv2LEOODt9VTN4OgvmVqLwXB+ZDZuj8K36GByWPhb7pHoFDO5DzDDc56p7iBVJEtg82aif7oK+EblqoacmzT63k1Pt0tqUE4LuWh5kH32bHZa+ZWsfbi91g+tpkktvMU87KRs80KzILm2DyGasxh4r3asKEW+Slo01540tXGfFzkyz0jzMQVjm3z/9J2uzKQFvQtUSSFV7TQCB7RAImMM4oIy7GKBd0rhrjS5sIgqCTarabu7ukmT0Yn+5Fqp/NCsNgujmBzEJxK3BucNGgKZ9dcOMlM1FkU8/dyLl599J2UlKg/FBaxMzPYTccb0fidTrYIR6JxUbMX4q54VtVlqgPQPC8JAclINo5qC2gNNCRqqZxr9EwVToLJGl4sK+UzTYIQl5SJ5rmUBitjIwjgOBi11MuQs7ztJgNT/3KlFXaqamZmGpdfHC4HvuX4YyVcYxvEpNcunGmqlpWweUO6Tp6lUzesIZGmeEqqmMixxGGSsObWC0xBhw3BHkatLufXQtYm11/zU8/akDjL1TdY8HY0sLx21CKEbMdSHjRf5GybBDOMUOI4Rw4LA9g/PokGxfMTi87RhVC8lhW7NTpTHsIEUdMpkHZvIo5dDFDmSOQwrNdGwAHBdylxIHUtYcqjfgW83+vRYq4LNgBzQ7JPnqdXL+VKbNzI0ZpZAjArGKSgsAGXAZhtiFCACX7rl0NT8o5cvjKOzwdsq3e8pQ3TG8udPy0y8fhp0mDbr+xrSBI5cjZRgZUjaSMdx32vBxE1sI8lPeANWciHz0qYP7CNO5ix27uRXWpx25Of2dmx6zumrq//3UU6h/GBbzuuyyw9ob7J3hr8H6ibcKQJdgAgCHmGBGym0DDCOAMXKx8lyus6ft/XhItrfYNkC3HftqIUPVZYAbS01KNleJzHTk0y8dRKnDwkC9KMVP5q+x8syAK+9czO9yqYE20m9IQS5xHA6w2zzj2yo18SFJjX7JSyY1Ww7Zd9303HgsItnuDdY3PSdPs+k53YQVUrwCrLnaV7oe4wzEAWyArt+kCBrm22cXPxVeaLWsw87F3ktkNSw/qSvitusSFWAg6iJIEYKsNCsEIpeVFmfPDGR6SGaFkmwiQEnLiUCDPFXXyNJYXksv6CA1HRbI6qVm8WReh9qclREJd5bS4biYYkghgICDPYVjcUjCUfoc0nIjbNXnfB8Fd9MorJ8nXjQtLb2Tqj3/CuZHHz/ArKJnvuCTwc0HuN05zfOfLcApG2wd8/cQw+tNFspzOSA7LWk+Sy7oBhdt02Hb31Pz4aHH235Ie/vd4pU0z+VA/Y4j8HtT0OrsziNxUH/eqwh+ntX5z+303DxHDdl+KvPo0BWm6h++k3Hc9OKBmw2/MPzSm0fJV7tsf+UFcfkjvZ3nrpei4Xbsla84Y7Zb/evz+pZaGC+aYLzoDuNFE4xtXtDQ6U0BLXHUbwqo24Db87UBtUCeNQF51h3Isz7y+BhAPtILhRoCv3z0WfhXXqAKlLWh4OqD/uqDXnmhA8N2hNQHhyvMPIMQcQu9HULERxlzHyfY2oyqyTd3CHS50n1E0aujYo6Oaw3rEeJr5UUO7SC95I6wshdtjxJatuSt4Z0SDXT+j0Wbz1XZ1jjjbmWGdrT+IhB80BTV565Q096ji7PNZOipKuyQ1+q957LGW7RP62zluG02VG88yneUQAiLs94qBHMxZy5GCGGtovvlu64/T75rFZiaZGi/A72ouh8TvrDQCwu/sM4vzjtITu/T3/ePJjmbGVHoIGUBOCQMUUJ4KSOUry7q7pkTvT8kGSlzonzLGwRbyEh1V+lwkVjEmkTBNLUW4UymqQhGXmyNpbCWB07sL/8IweoWtz91kKdHPwneRWSIzV2gt4swChmgqFjvx7ZDqcMQYI7LKEXN6/31qFa3kX4jJjLMFEPvBfwmFlLF+non9FSNPLzvgF7vnaWjD/CpwKU2oRA4KgCg0CEYFCsUSk2VPgIVanEHALTnCedRnjc7EH0kKItIOGxps1+u/hcJfV38x5mv/wtQSwcI8ERz8voNAACjZgAAUEsBAhQAFAAIAAgACqboPL1cAqreCwAAWw4AADEAAAAAAAAAAAAAAAAAAAAAAGI1YTFlNzczY2I3MzBjNzcwOWJhNWVhNmRjOGQ1Zjk2XEJld2Vpc3NjaGVtYS5wbmdQSwECFAAUAAgACAAKpug8IGKtYUkIAABzCgAAMQAAAAAAAAAAAAAAAAA9DAAANDYxNWE2MDE2YzMxNjhiM2I2MDc5ZWMzNTk1MDI1NGRcQmV3ZWlzc2NoZW1hLnBuZ1BLAQIUABQACAAIAAqm6DzwRHPy+g0AAKNmAAAMAAAAAAAAAAAAAAAAAOUUAABnZW9nZWJyYS54bWxQSwUGAAAAAAMAAwD4AAAAGSMAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| Zeile 116: | Zeile 67: | ||
Wir beweisen die Korrektheit der Konstruktion indem wir folgendes zeigen: | Wir beweisen die Korrektheit der Konstruktion indem wir folgendes zeigen: | ||
| − | ===== Satz VII.6 a: | + | ===== Satz VII.6 a: ===== |
::Wenn ein Punkt <math>\ P</math> zu den Endpunkten der Strecke <math>\overline{AB}</math> jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von <math>\overline{AB}</math>. | ::Wenn ein Punkt <math>\ P</math> zu den Endpunkten der Strecke <math>\overline{AB}</math> jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von <math>\overline{AB}</math>. | ||
| Zeile 140: | Zeile 91: | ||
Der folgende Satz VII.6 b beantwortet diese beiden Fragen postiv: | Der folgende Satz VII.6 b beantwortet diese beiden Fragen postiv: | ||
| − | ===== Satz VII.6 b | + | ===== Satz VII.6 b ===== |
::Wenn ein Punkt <math>\ P</math> zur Mittelsenkrechten der Strecke <math>\overline{AB}</math> gehört, dann hat er zu den Punkten <math>\ A</math> und <math>\ B</math> ein und denselben Abstand. | ::Wenn ein Punkt <math>\ P</math> zur Mittelsenkrechten der Strecke <math>\overline{AB}</math> gehört, dann hat er zu den Punkten <math>\ A</math> und <math>\ B</math> ein und denselben Abstand. | ||
| + | Beweis: Übungsaufgabe | ||
| + | ==Die Umkehrung des Basiswinkelsatzes== | ||
| + | ===== Satz VII.7===== | ||
| + | ::Wenn ein Dreieck zwei zueinander kongruente Innenwinkel hat, dann ist das Dreieck gleichschenklig. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
| + | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
| + | |} | ||
| + | </div> | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 27. Juni 2012, 12:11 Uhr
|
Der BasiswinkelsatzGleichschenklige DreieckeDefinition VII.4 : (gleichschenkliges Dreieck)Das können sie selbst. Bringen Sie in der Definition die Begriffe Basis, Basiswinkel und Schenkel eines gleichschenkligen Dreiecks unter. Übungsaufgabe Der BasiswinkelsatzSatz VII.5: Basiswinkelsatz
Schulvariante des Beweises des Basiswinkelsatzes Ein im Rahmen unserer Theorie korrekter Beweis des BasiswinkelsatzesProbieren Sie ruhig weitere Varianten: Mittelsenkrechte ... . Letztlich hilft nur die Winkelhalbierende des Winkels, der der Basis des gleichschenkligen Dreiecks gegenüberliegt. Die Winkelhalbierende muss dann die Basis des Dreiecks schneiden. Diese unmittelbar einsichtige Tatsache muss eigentlich bwiesen werden. Wir verweisen diesbezüglich auf die Lemmata zu Winkeln. Hinweis: Im folgenden Beweis berufen wir uns auf Lemma 1. Korrekterweise müsste es Lemma W/3 heißen. Sobald ich Zeit finde werde ich die App überarbeiten.--*m.g.* 18:17, 21. Jun. 2012 (CEST) Hier finden Sie das Arbeitsblatt zum Beweis des Basiswinkelsatzes aus der Vorlesung vom 28.06.2012. Beweis des Basiswinkelsatzes
Das MittelsenkrechtenkriteriumSatz VII.6: (Mittelsenkrechtenkriterium)
Bezug zur Schule:Konstruktion der Mittelsenkrechten einer Strecke Konstruktionsvorschrift: gegeben: Strecke gesucht:
Frage: Ist dieser Algorithmus korrekt? Anders gefragt: Ist Wir beweisen die Korrektheit der Konstruktion indem wir folgendes zeigen: Satz VII.6 a:
Beweis von Satz VII.6 aÜbungsaufgabe (Das Video hilft)
Die Wahl des Radius Die Frage anders formuliert: Hat jeder Punkt der Mittelsenkrechten von Noch anders formuliert: Hat jeder Punkt der Mittelsenkrechten einer Strecke Der folgende Satz VII.6 b beantwortet diese beiden Fragen postiv: Satz VII.6 b
Beweis: Übungsaufgabe Die Umkehrung des BasiswinkelsatzesSatz VII.7
|
 gehört genau dann zur Mittelsenkrechten der Strecke
gehört genau dann zur Mittelsenkrechten der Strecke  , wenn
, wenn 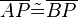 gilt.
gilt.
 , die Mittelsenkrechte von
, die Mittelsenkrechte von  , dessen Radius
, dessen Radius 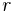 länger als die Hälfte der Länge der Strecke
länger als die Hälfte der Länge der Strecke  .
.
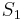 und
und 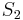 .
.
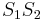 . Sie ist die gesuchte Mittelsenkrechte von
. Sie ist die gesuchte Mittelsenkrechte von 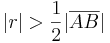 . Wir stellen uns jetzt die frage, ob wir jeden beliebigen Punkt unserer Mittelsenkrechten als Schnittpunkt zweier entsprechender Kreise konstruieren könnten.
. Wir stellen uns jetzt die frage, ob wir jeden beliebigen Punkt unserer Mittelsenkrechten als Schnittpunkt zweier entsprechender Kreise konstruieren könnten.

