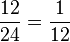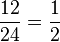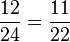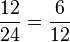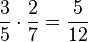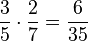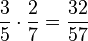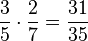Didaktische Konzepte II, 19.05.2015

Allgemein: Sinn und Zweck täglicher Übungen

Vor Beginn einer konkreten Unterrichtsstunde ist es sinnvoll diese mit täglichen Aufgaben zu starten, da die Schülerinnen und Schüler immer eine gewisse Zeit brauchen, bis sie in der Unterrichtsstunde ankommen. Durch den Einsatz von täglichen Aufgaben können die Schülerinnen und Schüler warm werden, sich auf die Stunde vorbereiten und zur Ruhe kommen.
Am besten ist es, wenn man den Schülerinnen und Schülern Aufgaben stellt, bei denen sie sich für die richtige Antwort entscheiden müssen. Somit setzen sie sich intensiv mit der "Materie" auseinander und der Frage, warum etwas falsch oder richtig ist (siehe Beispielaufgaben). Es ist allerdings darauf zu achten, dass die täglichen Übungen nicht zu schwer gestellt sind, da man den Schülerinnen und Schüler zu Beginn der Unterrichtsstunde eine positives Erlebnis ermöglichen möchte und sie erkennen, dass sie etwas können. Somit entwickeln sie eine positive Grundhaltung gegenüber der Unterrichtsstunde.
Ein weiterer Zweck von täglichen Übungen ist es, dass die Schülerinnen und Schüler den Stoff der letzten Stunden wiederholen können. Dies gibt dem Lehrer Rückschlüsse darauf, ob die Schülerinnen und Schüler den Stoff verinnerlicht haben und wo noch Schwierigkeiten bestehen. Man sollte jedoch den Schülern dabei vermitteln, dass Fehler nichts schlechtes sind, sondern dass man sie machen darf und lernt damit umzugehen.
Die letzte Aufgabe der täglichen Übung sollte immer auf das Thema der eigentlichen Unterrichtsstunde hinweisen.

Beispielaufgaben

Welche Brüche wurden richtig gekürzt?

• $\frac{12}{24} = \frac{1}{12}$
• $\frac{12}{24} = \frac{1}{2}$
• $\frac{12}{24}=\frac{11}{22}$
• $\frac{12}{24}= \frac{6}{12}$
  
  

Notiere die Aufgabe mit der richtigen Lösung.

• $\frac{3}{5} \cdot \frac{2}{7} = \frac{5}{12}$
  

• $\frac{3}{5} \cdot \frac{2}{7} = \frac{6}{35}$
  

• $\frac{3}{5} \cdot \frac{2}{7} = \frac{32}{57}$
  

• $\frac{3}{5} \cdot \frac{2}{7} = \frac{31}{35}$
  

Ergänze die folgende Regel:

• Multiplizieren ist echt der Renner.

Nimm Zähler mal Zähler und ...

Konzepte für die Bruchrechnung nach Padberg

Größenkonzept

Bei diesem Konzept geht man von konkreten Brüchen wie $\frac{1}{2}$ m, $\frac{3}{4}$ l oder $\frac{7}{8}$ km aus. Diese Brüche sind den Schülerinnen und Schülern aus dem alltäglichen Leben vertraut. Durch eine Abstraktion kommt man zu einer festen Größe als Bezugsgröße, welches das "Ganze" bzw. die "Einheit" darstellt.
Die Bruchzahl 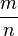$\frac{m}{n}$ ist hierbei eine Größe, die Größe 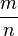$\frac{m}{n}$ E, wenn wir die Einheit E bezeichnen.

Vorteil

• Nähe zu vielen Anwendungen der Brüche im täglichen Leben => gute Rückgreifmöglichkeiten auf Vorkenntnisse
• Erweitern, Kürzen, Anordnungen, Addieren und Subtrahieren lassen sich gut von alltäglichen Anwendungssituationen her motivieren und anschaulich behandeln
  

Nachteil

• hat seine Grenzen bei der Multiplikation => Umdeutung des Bruchbegriffs erforderlich, da für Größen im natürliche Sinne keine Multiplikation erklärbar ist
• Grenzen bei der Division => Ergebnis ist keine Größe, also keine Bruchzahl im Sinne des Konzepts

Gleichungskonzept

Die Bruchzahl 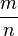$\frac{m}{n}$ ist bei diesem Konzept die Lösung einer linearen Gleichung 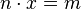$n \cdot x = m$, wobei 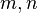$m,n$ natürliche Zahlen sind. Die Lösung dieser Gleichung schreibt man auch 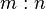$m : n$, so erhält man die Beziehung $m:n = \frac{m}{n}$.

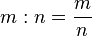Vorteil

• Erweitern, Kürzen und die Rechenoperationen sind gut einführbar
  

z.B Addition zweier Brüche: 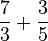$\frac{7}{3} + \frac{3}{5}$
Definitionsgleichungen: 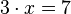$3 \cdot x = 7$ und $5 \cdot y = 3$
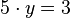
Gleichung finden für 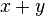$x + y$ (erweitern): $15 \cdot x = 35$ , $15 \cdot y = 9$ => $x+y = \frac{44}{15}$
=> $\frac{7}{3}+ \frac{3}{5} = \frac{44}{15}$

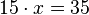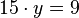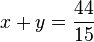
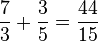
Nachteil

• belastet spätere Behandlung der Gleichungslehre
• für die Schülerinnen und Schüler ist dieses Verständnis einer Bruchzahl noch zu schwer
• Einführung der Division bereitet Schwierigkeiten
• Anwendung der Bruchzahlen als Maßzahlen von Größen schwer erklärbar