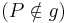13)
Inhaltsverzeichnis |
Ideen zur Heranführung an die Geradenspiegelung
Idee der Symmetrie
Die Applikation wurde im WS 2010/11 von tutorin Anne generiert.
Verwendung eines halbdurchlässigen Spiegels
 |
 |

|
 |
 |

|
 |
 |

|
 |
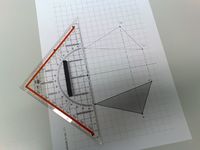 |
Falten
Leider sind meine Bilder von der Qualität her zu schlecht geworden, als dass sie hier veröffentlicht werden könnten. Wer hilft? --*m.g.* 13:04, 27. Okt. 2011 (CEST)
Konstruktion des Bildes eines Punktes  bei einer Spiegelung an der Geraden
bei einer Spiegelung an der Geraden 
Reduktion der großen Idee Geradenspiegelung auf: Konstruktion des Bildes eines Punktes bei einer Geradenspiegelung
Übungsaufgabe:
Es sei  ein Punkt der Ebene der nicht zur Geraden
ein Punkt der Ebene der nicht zur Geraden  dieser Ebene gehört.
Erstellen Sie eine Konstruktionsbeschreibung für die Konstruktion des Bildes von
dieser Ebene gehört.
Erstellen Sie eine Konstruktionsbeschreibung für die Konstruktion des Bildes von  bei der Spiegelung an
bei der Spiegelung an  . Begründen Sie jeweils die Korrektheit eines jeden Ihrer Konstruktionsschritte.
. Begründen Sie jeweils die Korrektheit eines jeden Ihrer Konstruktionsschritte.
| Nr. | Beschreibung des Schrittes | Genauere Beschreibung | Begründung der Korrektheit des Schrittes |
|---|---|---|---|
| 1. | ... | ... | ... |
| 2. | ... | ... | ... |
| 3. | ... | ... | ... |
Bemerkung zum Nachweis der Korrektheit des jeweiligen Schrittes: Gemeint ist eine Begründung, aus der hervorgeht, dass der jeweilige Schritt (ggf. eindeutig) ausführbar ist.
Definition des Begriffs
Definition 2.1: (Spiegelung an der Geraden  )
)
- Es sei
 eine Gerade. Unter der Spiegelung
eine Gerade. Unter der Spiegelung 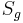 an der Geraden
an der Geraden  versteht man eine Abbildung der Ebene auf sich, ...
versteht man eine Abbildung der Ebene auf sich, ...
- Es sei
Die Geradenspiegelung als spezielle Bewegung
Satz 2.1: (Abstandserhaltung von Geradenspiegelungen)
- Jede Geradenspiegelung
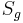 ist eine abstandserhaltende Abbildung.
ist eine abstandserhaltende Abbildung.
- Jede Geradenspiegelung
Beweis von Satz 2.1:
Es seien  ,
,  zwei Punkte, die an einer Geraden
zwei Punkte, die an einer Geraden  auf ihre Bilder
auf ihre Bilder 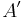 und
und 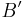 gespiegelt werden.
gespiegelt werden.
Wir unterscheiden drei Fälle:
Fall 1
Beweis:
Fall 2


 ,
, 
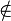

Beweis:
Fall 3

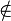
 ,
,  und
und  liegen in derselben Halbebene bezüglich
liegen in derselben Halbebene bezüglich 
Beweis:
Fall 4

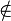
 ,
,  und
und  liegen in verschiedenen Halbebenen bezüglich
liegen in verschiedenen Halbebenen bezüglich 
Eindeutige Bestimmtheit von Geradenspiegelungen
Bestimmung über die Spiegelgerade
Unmittelbar einsichtig ist der folgende Satz:
Satz 2.2
- Jede Geradenspiegelung ist durch die Angabe ihrer Spiegelachse eindeutig bestimmt.
- Jede Geradenspiegelung ist durch die Angabe ihrer Spiegelachse eindeutig bestimmt.
Satz 2.3
- Eine Geradenspiegelung
 ist durch die Angabe eines Punktes
ist durch die Angabe eines Punktes  und dem Bild von
und dem Bild von 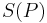 eindeutig bestimmt, falls
eindeutig bestimmt, falls 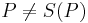 gilt.
gilt.
- Eine Geradenspiegelung