Halbebenen oder das Axiom von Pasch: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Analogiebetrachtungen) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 18: | Zeile 18: | ||
| <math>\ G</math> ist eine ... | | <math>\ G</math> ist eine ... | ||
| − | | | + | |- |
| − | + | ||
| − | + | ||
| colspan="2" style="background: #DDFFDD;"| <center>Dimension von <math>\ G</math></center> | | colspan="2" style="background: #DDFFDD;"| <center>Dimension von <math>\ G</math></center> | ||
| Zeile 35: | Zeile 33: | ||
| <math>\ T</math> ist ... | | <math>\ T</math> ist ... | ||
| − | | | + | |- |
| − | + | ||
| − | + | ||
| colspan="2" style="background: #DDFFDD;"| <center>Dimension von <math>\ T</math></center> | | colspan="2" style="background: #DDFFDD;"| <center>Dimension von <math>\ T</math></center> | ||
| Zeile 44: | Zeile 40: | ||
| <math>\ T</math> hat die Dimension ... | | <math>\ T</math> hat die Dimension ... | ||
| − | | | + | |- |
| − | + | ||
| − | + | ||
| colspan="2" style="background: #DDFFDD; "| <center>Referenzpunkt <math>\ Q</math> teilt <math>\ G \setminus_{\{ Q \}}</math> in genau zwei Klassen</center> | | colspan="2" style="background: #DDFFDD; "| <center>Referenzpunkt <math>\ Q</math> teilt <math>\ G \setminus_{\{ Q \}}</math> in genau zwei Klassen</center> | ||
|- | |- | ||
| − | | colspan="2" | <center>Klasse 1: </center> | + | | colspan="2" | |
| − | + | <center>Klasse 1: </center> | |
<center>Menge aller Punkte <math>\ P\mathrm{\in }G</math> , die mit <math>\ Q</math> bezüglich <math>\ T</math> „auf derselben Seite liegen“</center> | <center>Menge aller Punkte <math>\ P\mathrm{\in }G</math> , die mit <math>\ Q</math> bezüglich <math>\ T</math> „auf derselben Seite liegen“</center> | ||
Version vom 2. Juni 2010, 14:25 Uhr
Halbebenen
Analogiebetrachtungen
| |
|
 , das in Klassen eingeteilt wird , das in Klassen eingeteilt wird | |
 ist eine ... ist eine ...
|
 ist eine ... ist eine ...
|
 | |
| Dimension von | Dimension von |
 , das , das  in Klassen einteilt in Klassen einteilt | |
 ist ... ist ...
|
 ist ... ist ...
|
 | |
 hat die Dimension ... hat die Dimension ...
|
 hat die Dimension ... hat die Dimension ...
|
 teilt teilt 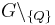 in genau zwei Klassen in genau zwei Klassen | |
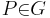 , die mit , die mit  bezüglich bezüglich  „auf derselben Seite liegen“ „auf derselben Seite liegen“ | |
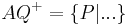
|
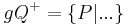
|
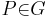 , die bezüglich , die bezüglich  nicht auf der Seite von nicht auf der Seite von  liegen. liegen. | |
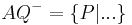
|
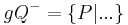
|

